4/52 = 1/13 - вероятность выбрать взять карту «короля»
теперь надо расписать все возможные варианты для 5 карт
К - король; Х - не король:
вообще в данном случае много вариантов, поэтому я напишу только один вариант, который не подходит, ведь только при одном варианте королей вообще не будет: Х Х Х Х Х
вероятность этого события надо вычислить и вычесть и 1 (100%)
вероятность достать карту не с королем = 1 - 1/13 = 12/13
так как мы достаем 5 карт, то вероятность (Х Х Х Х Х) =
Описание процедуры дележа начнем со случая, когда число участвующих в нем пиратов равно двум. В этом случае старший из двух пиратов забирает все золото – половина (он сам) поддерживает его предложение. Итог дележа (0, 0, 0, 10, 0). В случае, когда число пиратов равно трем, старший из трех предлагает дележ, дающий 9 слитков ему и 1 слиток младшему. Младший, понимая, что иначе ему вообще ничего не достанется, вынужден этот дележ поддержать. Итог дележа (0, 0, 9, 0, 1). В случае, когда число пиратов равно четырем, старший из четырех рассуждает так: «Если мое предложение будет отвергнуто, то три оставшихся пирата разделят слитки по правилу (9, 0, 1); следовательно, я должен предложить такой дележ, который был бы выгоднее хотя бы одному из них и максимизировал бы мою долю. Такой дележ (0, 9, 0, 1, 0). Рассуждая аналогично для пяти пиратов, получаем ответ (8, 0, 1, 0, 1)
0,33
Пошаговое объяснение:
4/52 = 1/13 - вероятность выбрать взять карту «короля»
теперь надо расписать все возможные варианты для 5 карт
К - король; Х - не король:
вообще в данном случае много вариантов, поэтому я напишу только один вариант, который не подходит, ведь только при одном варианте королей вообще не будет: Х Х Х Х Х
вероятность этого события надо вычислить и вычесть и 1 (100%)
вероятность достать карту не с королем = 1 - 1/13 = 12/13
так как мы достаем 5 карт, то вероятность (Х Х Х Х Х) =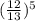
что примерно равняется 0,67
теперь из 100% вычитаем полученные 67%
1 - 0,67 = 0,33
ответ: (8, 0, 1, 0, 1
Пошаговое объяснение:
Описание процедуры дележа начнем со случая, когда число участвующих в нем пиратов равно двум. В этом случае старший из двух пиратов забирает все золото – половина (он сам) поддерживает его предложение. Итог дележа (0, 0, 0, 10, 0). В случае, когда число пиратов равно трем, старший из трех предлагает дележ, дающий 9 слитков ему и 1 слиток младшему. Младший, понимая, что иначе ему вообще ничего не достанется, вынужден этот дележ поддержать. Итог дележа (0, 0, 9, 0, 1). В случае, когда число пиратов равно четырем, старший из четырех рассуждает так: «Если мое предложение будет отвергнуто, то три оставшихся пирата разделят слитки по правилу (9, 0, 1); следовательно, я должен предложить такой дележ, который был бы выгоднее хотя бы одному из них и максимизировал бы мою долю. Такой дележ (0, 9, 0, 1, 0). Рассуждая аналогично для пяти пиратов, получаем ответ (8, 0, 1, 0, 1)