где — абсцисса точки графика функции , к которому проведена касательная .
Так как график касательной имеет вид график прямой линейной функции , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
Таким образом, касательная будет горизонтальной, если
Найдем :
Найдем :
Следовательно, — абсцисса точки графика функции , к которому проведена касательная .
Найдем значение :
Таким образом, — уравнение горизонтальной касательной к графику функции
Область определения : - оо ; оо Ассимптоты : нет Макс. или мин. : y '=4*x^3 - 16x =4x*(x^2 - 4)=0 x1= -2 ; x2=0 ; x3=2 при - oo <х < -2 y ' <0 -- функция убывает при -2 <х <0 y '>0 -- функция возрастает т. е. имеет мин. вточке х= -2 при 0 <х <2 y ' <0 -- функция убывает т. е. имеет макс. в точке х=0 при х>2 y '>0 -- функция возрастает т. е. имеет мин. вточке х= 2 Перегибы : y''=12x^2 - 16=0 x=±2 /√3 x1= -1.15 ; x2=1.15 при -oo <х < -1.15 y''>0 -- функция вогнутая при -1.15 <х < 1.15 y'' <0 -- функция выпуклая т. е. имеет перегиб в точке х= -1.15 при х>1.15 y''>0 -- функция вогнутая т. е. имеет перегиб в точке х=1.15
Уравнение касательной имеет вид:
где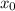 — абсцисса точки графика функции
— абсцисса точки графика функции 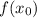 , к которому проведена касательная
, к которому проведена касательная 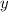 .
.
Так как график касательной имеет вид график прямой линейной функции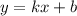 , а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции — 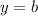
Таким образом, касательная будет горизонтальной, если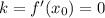
Найдем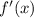 :
:
Найдем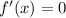 :
:
Следовательно,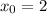 — абсцисса точки графика функции
— абсцисса точки графика функции 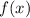 , к которому проведена касательная
, к которому проведена касательная 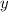 .
.
Найдем значение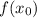 :
:
Таким образом,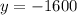 — уравнение горизонтальной касательной к графику функции
— уравнение горизонтальной касательной к графику функции 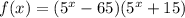
ответ: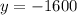
Ассимптоты : нет
Макс. или мин. : y '=4*x^3 - 16x =4x*(x^2 - 4)=0 x1= -2 ; x2=0 ; x3=2
при - oo <х < -2 y ' <0 -- функция убывает
при -2 <х <0 y '>0 -- функция возрастает т. е. имеет мин. вточке х= -2
при 0 <х <2 y ' <0 -- функция убывает т. е. имеет макс. в точке х=0
при х>2 y '>0 -- функция возрастает т. е. имеет мин. вточке х= 2
Перегибы : y''=12x^2 - 16=0 x=±2 /√3 x1= -1.15 ; x2=1.15
при -oo <х < -1.15 y''>0 -- функция вогнутая
при -1.15 <х < 1.15 y'' <0 -- функция выпуклая т. е. имеет перегиб в точке х= -1.15
при х>1.15 y''>0 -- функция вогнутая т. е. имеет перегиб в точке х=1.15