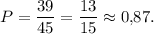Статистические данные показывают , что за 12 месяцев текущего года в одной из областей родилось 8355 детей , что на 476 детей , или на P% , больше, чем в январе-октябре. Найдите р .
1) проведём высоты nh и ks. ⇒ угол mhn=90° и угол ksp=90°⇒треугольники mhn и pks - прямоугольные. 2) mh/mn=sin45° mh/8=корень из 2/2 mh=4 корней из 2 3)sp/kp=sin30° sp/10=1/2 sp=5 4) hnks - прямоугольник, т.к hnks является параллелограммом (nk параллельно hs, т.к основания трапеции параллельны и nh параллельно ks по соответственно равным ∠ 90° = nhm и ksm), у которого все ∠ равны по 90° значит nk=hp=5 см отсюда mp=mh+hs+sp= 4√2 + 5 + 5 = 10 + 4√2 (см) 5) средняя линия bd = (nk + mp)/2= (5 + 10 + 4√2)/2 = 7,5 + 2 √2 ответ: 7,5 + 2√ 2
Задача. Фирма среди своих сотрудников разыгрывает новогоднюю лотерею. В лотерее 10 билетов, из которых 6 выигрышных. Сотрудник фирмы покупает 2 билета. Какова вероятность того, что у этого сотрудника выиграет хотя бы один билет? Результат округлите до сотых.
Количество возможных элементарных исходов равно числу вынуть два билета из 10 билетов, т.е. .
Подсчитаем количество благоприятных исходов. Для этого нужно определить сколькими этот сотрудник может выбрать хотя бы один выигрышный билет. Таких
Задача. Фирма среди своих сотрудников разыгрывает новогоднюю лотерею. В лотерее 10 билетов, из которых 6 выигрышных. Сотрудник фирмы покупает 2 билета. Какова вероятность того, что у этого сотрудника выиграет хотя бы один билет? Результат округлите до сотых.
Количество возможных элементарных исходов равно числу вынуть два билета из 10 билетов, т.е.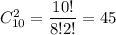 .
.
Подсчитаем количество благоприятных исходов. Для этого нужно определить сколькими этот сотрудник может выбрать хотя бы один выигрышный билет. Таких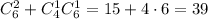
Искомая вероятность: