y"=2y' - это линейное однородное ДУ второго порядка с постоянными коэффициентами.
y"-2y'=0 (1)
Составим и решим характеристическое уравнение:
р²-2p=0
p*(p-2)=0
p₁=0
p₂=2
Получены два различных действительных корня, поэтому общее решение имеет вид:
y=C₁*e^(p₁*x)+C₂*e^(p₂*x), где p₁ и p₂ - корни характеристического уравнения, C₁ и C₂ - константы.
y=C₁*e^(0*x)+C₂*e^(2*x)
y=C₁+C₂*e^(2*x) - общее решение (2).
Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти такие значения констант С₁ и С₂, чтобы выполнялись оба условия.
Сначала используем начальное условие y(0)=3/2:
y(0)=C₁+C₂*e^(2*0)=C₁+C₂
Согласно начальному условию получаем первое уравнение:
C₁+C₂=3/2 (3)
Далее берем общее решение (2) и находим производную:
1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3.
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4.
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:
d²y/dx²=2*dy/dx
Можно переписать:
y"=2y' - это линейное однородное ДУ второго порядка с постоянными коэффициентами.
y"-2y'=0 (1)
Составим и решим характеристическое уравнение:
р²-2p=0
p*(p-2)=0
p₁=0
p₂=2
Получены два различных действительных корня, поэтому общее решение имеет вид:
y=C₁*e^(p₁*x)+C₂*e^(p₂*x), где p₁ и p₂ - корни характеристического уравнения, C₁ и C₂ - константы.
y=C₁*e^(0*x)+C₂*e^(2*x)
y=C₁+C₂*e^(2*x) - общее решение (2).
Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти такие значения констант С₁ и С₂, чтобы выполнялись оба условия.
Сначала используем начальное условие y(0)=3/2:
y(0)=C₁+C₂*e^(2*0)=C₁+C₂
Согласно начальному условию получаем первое уравнение:
C₁+C₂=3/2 (3)
Далее берем общее решение (2) и находим производную:
y'=(C₁+C₂*e^(2*x))'=0+2*C₂*e^(2*x)=2*C₂*e^(2*x)
Используем второе начальное условие y'(0)=1:
y'(0)=2*C₂*e^(2*0)=2*C₂
2*C₂=1
C₂=1/2 (4)
Теперь поддставим (4) в (3):
C₁+1/2=3/2
C₁=1 (5)
Остается подставить (4) и (5) в (2):
y=1+3/2*e^(2*x) - частное решение.
ответ: y=C₁+C₂*e^(2*x) - общее решение
y=1+3/2*e^(2*x) - частное решение
Подробнее - на -
Пошаговое объяснение:
1. б) (-3; 8]
2. а)
3. x∈ [-1; 2)
4. x∈ (-3; +∞)
5. x∈ (-1,5; 6]
6. x∈ [1/5; 2]
7. x∈ (-∞; 12]
8. x∈ [-2; 3]
Пошаговое объяснение:
1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3.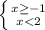
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4.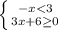
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:
1/5 ≤ x ≤ 2 или x∈ [1/5; 2]
7. Решите совокупность неравенств
Отсюда х ≤ 12 или x∈ (-∞; 12]
8.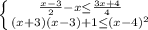
Отсюда -2 ≤ х ≤ 3 или x∈ [-2; 3]