а) Таблица отношения (никогда таким не занимался, думаю, она должна выглядеть примерно так):
1 | 2 | 3 | 4
1 * | | | *
2 | * | * |
3 | * | * |
4 * | | | *
Область определения — X = {1, 2, 3, 4}. Область значений — Y = {1, 2, 3, 4}.
б) Отношение рефлексивно, т. к. : есть пары (1; 1), (2; 2), (3; 3), (4; 4).
Отношение не антирефлексивно, т. к.
Отношение симметрично, т. к. : (1; 4) — (4; 1), (2; 3) — (3; 2) + все пары вида (x; x).
Отношение не антисимметрично, т. к. : (2; 3) и (3; 2).
Отношение транзитивно, т. к. : (1; 1), (1; 4) — (1; 4); (1; 4), (4; 4) — (1; 4); (1; 4), (4; 1) — (1; 1); (4; 1), (1; 4) — (4; 4). Аналогично с 2 и 3.
в) P является отношением эквивалентности, т. к. рефлексивно, симметрично, транзитивно. P не является отношением порядка, так как не антисимметрично.
Отношение не является функцией, т. к. , например, (1; 1), (1; 4).
↓↓↓
Пошаговое объяснение:
у=х³-9\2*х²+6х-2
у=х³-4,5х²+6х-2. Область определения х-любое.
1)Промежутки возрастания и убывания.
Найдем производную функции
у'=(х³-4,5х²+6х-2)'=3х²-9х+6=3(х²-3х+2)=3(х-2)(х-1).
Критические точки х=2,х=1 , при у'=0. Функция возрастает если у'>0
3(х-2)(х-1)>0
++++++++++(1)- -- -- -- - -- -(2)++++++++ , х∈(-∞;1) и (2;+∞) .
Т.к. функция определена и непрерывна при любом х, то можно включит концы отрезка х∈(-∞;1] и [2;+∞)
Функция убывает если у'<0 ⇒ х∈[1;2] .
2)Экстремумы функции у=х³-4,5х²+6х-2.
у' + - +
-----------------------(1)---------------------------(2)---------------
у возр max убыв min возр
х=1 точка максимума , у(1)=1³-4,5*1²+6*1 -2=1- 4,5+6-2=0,5
х=2 точка минимума , у(2)=2³-4,5*2²+6*2 -2= 0.
а) Таблица отношения (никогда таким не занимался, думаю, она должна выглядеть примерно так):
1 | 2 | 3 | 4
1 * | | | *
2 | * | * |
3 | * | * |
4 * | | | *
Область определения — X = {1, 2, 3, 4}. Область значений — Y = {1, 2, 3, 4}.
б) Отношение рефлексивно, т. к.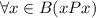 : есть пары (1; 1), (2; 2), (3; 3), (4; 4).
: есть пары (1; 1), (2; 2), (3; 3), (4; 4).
Отношение не антирефлексивно, т. к.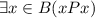
Отношение симметрично, т. к.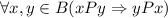 : (1; 4) — (4; 1), (2; 3) — (3; 2) + все пары вида (x; x).
: (1; 4) — (4; 1), (2; 3) — (3; 2) + все пары вида (x; x).
Отношение не антисимметрично, т. к.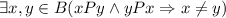 : (2; 3) и (3; 2).
: (2; 3) и (3; 2).
Отношение транзитивно, т. к.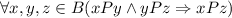 : (1; 1), (1; 4) — (1; 4); (1; 4), (4; 4) — (1; 4); (1; 4), (4; 1) — (1; 1); (4; 1), (1; 4) — (4; 4). Аналогично с 2 и 3.
: (1; 1), (1; 4) — (1; 4); (1; 4), (4; 4) — (1; 4); (1; 4), (4; 1) — (1; 1); (4; 1), (1; 4) — (4; 4). Аналогично с 2 и 3.
в) P является отношением эквивалентности, т. к. рефлексивно, симметрично, транзитивно. P не является отношением порядка, так как не антисимметрично.
Отношение не является функцией, т. к.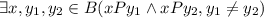 , например, (1; 1), (1; 4).
, например, (1; 1), (1; 4).
↓↓↓
Пошаговое объяснение:
у=х³-9\2*х²+6х-2
у=х³-4,5х²+6х-2. Область определения х-любое.
1)Промежутки возрастания и убывания.
Найдем производную функции
у'=(х³-4,5х²+6х-2)'=3х²-9х+6=3(х²-3х+2)=3(х-2)(х-1).
Критические точки х=2,х=1 , при у'=0. Функция возрастает если у'>0
3(х-2)(х-1)>0
++++++++++(1)- -- -- -- - -- -(2)++++++++ , х∈(-∞;1) и (2;+∞) .
Т.к. функция определена и непрерывна при любом х, то можно включит концы отрезка х∈(-∞;1] и [2;+∞)
Функция убывает если у'<0 ⇒ х∈[1;2] .
2)Экстремумы функции у=х³-4,5х²+6х-2.
у' + - +
-----------------------(1)---------------------------(2)---------------
у возр max убыв min возр
х=1 точка максимума , у(1)=1³-4,5*1²+6*1 -2=1- 4,5+6-2=0,5
х=2 точка минимума , у(2)=2³-4,5*2²+6*2 -2= 0.