Формула площади трапеции через стороны (вывод ниже):
Объем прямой призмы равен произведению площади основания S на высоту призмы h:
ответ: Объем призмы равен 3690 см³.
_______________________________
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y. Таким образом x+y = d−b, y = d−b−x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем:
a²−x² = c²−y² или x²−y² = a²−c².
Подставляем вместо х полученное выше выражение d−b−x:
x²−(d−b−x)² = a²−c²
x²−d²+bd+dx-b²+bd−bx−x²+dx−bx = a²−c²
x²−d²+2bd+2dx−b²−2bx−x² = a²−c²
2dx−2bx = a²−c²+d²+b²−2bd
2x(d−b)=a²−c²+(d−b)²
Подставляем обратно x в формулу высоты:
Формула площади трапеции через стороны будет выглядеть так:
Формула площади трапеции через стороны (вывод ниже):
Объем прямой призмы равен произведению площади основания S на высоту призмы h:
ответ: Объем призмы равен 3690 см³.
_______________________________
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y. Таким образом x+y = d−b, y = d−b−x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту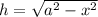
и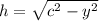 
. Приравнивая, получаем:
a²−x² = c²−y² или x²−y² = a²−c².
Подставляем вместо х полученное выше выражение d−b−x:
x²−(d−b−x)² = a²−c²
x²−d²+bd+dx-b²+bd−bx−x²+dx−bx = a²−c²
x²−d²+2bd+2dx−b²−2bx−x² = a²−c²
2dx−2bx = a²−c²+d²+b²−2bd
2x(d−b)=a²−c²+(d−b)²
Подставляем обратно x в формулу высоты:
Формула площади трапеции через стороны будет выглядеть так:
Пошаговое объяснение:
1. 4с(с-2)-(с-4)²=4с²-8с-с²+8с-16=3с²-16
2. 2(3х-7)-5х≤3х-11
6х-14-5х-3х+11≤0
-2х-3≤0
2х+3≥0
2х≥-3
х≥-3/2
х≥-1,5
х∈[-1,5;+∞)
3.
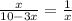
x²+3x-10=0
x₁=-5
x₂=2
5. 2x²-3x-2=(2x+1)(x-2)
6. 9 класс = х
10 класс = 0,8х
х+0,8х=162
1,8х=162
х=90
9 класс = 90 учеников
10 класс = 90*0,8 = 72 ученика
7.
< 
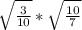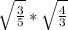
8.
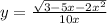
Область определения: x∈[-3;0)∪(0;0,5]
9.bₙ=√bₙ₊₁*bₙ₋₁
q=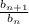
b₃=12
q=2
b₁=3
b₈=384
S₈=765
10. x -сторона квадрата
х+40 - длина прямоугольника
х-30 - ширина прямоугольника
(х+40)(х-30)=х²
х²+40х-30х-1200=х²
10х=1200
х=120
ответ: 120 метров сторона квадратного участка