Существует
Пошаговое объяснение:
Попробуем предъявить такой многочлен. В точке 0 значение должно быть 19, так что многочлен должен иметь вид .
Подставляем x = 1: , тогда и .
Подставляем найденное Q в P:
Теперь подставляем x = 2:
Самый простой удовлетворить такому требованию - взять R(x) = 917 тождественно, тогда получится полином
Можно получить и общий вид многочленов, удовлетворяющих условию. Для этого надо взять . Получим, что подойдут полиномы вида
,
где многочлен S(x) можно выбрать произвольно
Существует
Пошаговое объяснение:
Попробуем предъявить такой многочлен. В точке 0 значение должно быть 19, так что многочлен должен иметь вид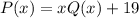 .
.
Подставляем x = 1: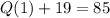 , тогда
, тогда 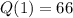 и
и 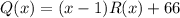 .
.
Подставляем найденное Q в P: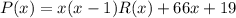
Теперь подставляем x = 2:
Самый простой удовлетворить такому требованию - взять R(x) = 917 тождественно, тогда получится полином
Можно получить и общий вид многочленов, удовлетворяющих условию. Для этого надо взять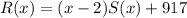 . Получим, что подойдут полиномы вида
. Получим, что подойдут полиномы вида
где многочлен S(x) можно выбрать произвольно