Решаем с РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ ПУТЕМ ГРУППИРОВКИ
Используем бинома Ньютона.
Чтобы найти противоположное значение выражения y²
+8y+16, необходимо найти противоположное значение для каждого члена.
Приводим многочлен к стандартному виду. Размещаем члены, начиная с члена с наибольшей степенью и заканчивая членом с наименьшей степенью.
Чтобы решить уравнение, разложите левую сторону на множители путем группировки. Сначала левую сторону необходимо перезаписать в следующем виде: -y²+ay+by-4.Чтобы найти a и b, настраиваем систему для решения.
Поскольку ab положительное, a и b имеют одинаковый знак. Так как a+b отрицательный, a и b являются отрицательными. Перечисляем все такие пары, содержащие 4 продукта.
Вычисляем сумму для каждой пары.
Решение — это пара значений, сумма которых равна −5.
Переписываем -y²-5y-4 как (-y²-y)+(-4y-4).
Выносим за скобки y в первой и 4 во второй группе.
Выносим за скобки общий член −y−1, используя свойство дистрибутивности.
Чтобы найти решения для уравнений, решаем −y−1=0 и y+4=0.
Дано, что точка К находится на одинаковом расстоянии от сторон КА и КВ прямого угла С. Мы знаем, что прямой угол состоит из двух перпендикулярных сторон.
Для начала, давайте построим данную ситуацию на рисунке для лучшего понимания.
(Далее следует пояснение с помощью изображений для лучшего понимания задачи.)
Теперь, нам нужно доказать, что четырехугольник ОАСВ является квадратом.
Для этого, давайте рассмотрим триугольники ОАК и ОВК.
У нас есть:
1) КА = КВ (из условия задачи)
2) КО = КО (так как О является проекцией К на плоскость угла С)
Давайте рассмотрим два случая:
1) Допустим, ОА ≠ ОВ. В этом случае, у нас есть две разные длины сторон ОА и ОВ. Назовём их а и b соответственно.
Теперь, посмотрим на треугольники ОАК и ОВК. У них есть:
1) ОА = ОВ (так как обе стороны равны а и b соответственно)
2) КА = КВ (из условия задачи)
3) КО = КО (так как О является проекцией К на плоскость угла С)
Из этих равенств, мы можем заключить, что треугольники ОАК и ОВК являются равнобедренными.
Теперь, давайте рассмотрим углы этих треугольников. У них есть:
1) Угол ОАК = Угол ОКА (так как треугольник ОАК равнобедренный)
2) Угол ОВК = Угол ОКВ (так как треугольник ОВК равнобедренный)
3) Угол ОКА = Угол ОКВ (так как треугольники ОАК и ОВК базируются на каждой стороне КО)
Теперь имея все эти равенства углов, мы можем заключить, что углы треугольника ОАК равны углам треугольника ОВК. Из этого следует, что треугольники ОАК и ОВК являются подобными (по признаку угол-угол-угол).
Зная, что треугольники ОАК и ОВК являются подобными и имеют равные основания (КА = КВ), мы можем сделать вывод, что их высоты тоже равны. Значит, точки ОА и ОВ лежат на одной горизонтальной линии, что противоречит нашему исходному предположению ОА ≠ ОВ.
2) Теперь давайте рассмотрим второй случай, когда ОА = ОВ.
В этом случае, мы имеем две равные стороны ОА и ОВ, а также равные стороны КА и КВ (из условия задачи).
Зная это, мы можем заключить, что треугольники ОАК и ОВК являются равнобедренными треугольниками (из определения равнобедренного треугольника).
Также, мы знаем, что углы КАО и КВО являются прямыми, так как они образованы перпендикулярными сторонами прямого угла С.
Таким образом, мы можем сделать вывод, что у треугольников ОАК и ОВК равные углы при основании, а также соответственно равные углы при вершине.
Так как, в треугольниках у нас имеются равные стороны и равные углы при основании и вершине, то они полностью равны друг другу.
Окончательно, мы можем заключить, что треугольники ОАК и ОВК равны друг другу.
Теперь давайте рассмотрим четырехугольник ОАСВ. У нас есть:
1) ОА = ОВ (из условия задачи)
2) АС = ВС (сторона угла С)
Поскольку стороны ОА и ОВ равны, а стороны АС и ВС равны, мы можем заключить, что ОАСВ является прямоугольником по определению прямоугольника.
Также, у нас есть следующая информация:
1) Угол ОАС = Угол ОВС (так как углы опираются на равные стороны ОА и ОВ)
2) Угол ОСА = Угол ОСВ (так как углы опираются на равные стороны АС и ВС)
3) Угол ОАС + Угол ОСА = 90 градусов (из определения прямоугольника)
Из этих равенств, мы можем заключить, что все углы четырехугольника ОАСВ являются прямыми углами.
Таким образом, мы доказали, что четырехугольник ОАСВ является квадратом по определению квадрата (имеет равные стороны и прямые углы).
Это и есть доказательство того, что ОАСВ является квадратом.
Решаем с РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ ПУТЕМ ГРУППИРОВКИ
Используем бинома Ньютона.
Чтобы найти противоположное значение выражения y²
+8y+16, необходимо найти противоположное значение для каждого члена.
Приводим многочлен к стандартному виду. Размещаем члены, начиная с члена с наибольшей степенью и заканчивая членом с наименьшей степенью.
Чтобы решить уравнение, разложите левую сторону на множители путем группировки. Сначала левую сторону необходимо перезаписать в следующем виде: -y²+ay+by-4.Чтобы найти a и b, настраиваем систему для решения.
Поскольку ab положительное, a и b имеют одинаковый знак. Так как a+b отрицательный, a и b являются отрицательными. Перечисляем все такие пары, содержащие 4 продукта.
Вычисляем сумму для каждой пары.
Решение — это пара значений, сумма которых равна −5.
Переписываем -y²-5y-4 как (-y²-y)+(-4y-4).
Выносим за скобки y в первой и 4 во второй группе.
Выносим за скобки общий член −y−1, используя свойство дистрибутивности.
Чтобы найти решения для уравнений, решаем −y−1=0 и y+4=0.
1)−y−1=0
−y=1
y=−1
2) y+4=0
y=−4
ответ: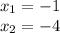
Пошаговое объяснение:
Дано, что точка К находится на одинаковом расстоянии от сторон КА и КВ прямого угла С. Мы знаем, что прямой угол состоит из двух перпендикулярных сторон.
Для начала, давайте построим данную ситуацию на рисунке для лучшего понимания.
(Далее следует пояснение с помощью изображений для лучшего понимания задачи.)
Теперь, нам нужно доказать, что четырехугольник ОАСВ является квадратом.
Для этого, давайте рассмотрим триугольники ОАК и ОВК.
У нас есть:
1) КА = КВ (из условия задачи)
2) КО = КО (так как О является проекцией К на плоскость угла С)
Давайте рассмотрим два случая:
1) Допустим, ОА ≠ ОВ. В этом случае, у нас есть две разные длины сторон ОА и ОВ. Назовём их а и b соответственно.
Теперь, посмотрим на треугольники ОАК и ОВК. У них есть:
1) ОА = ОВ (так как обе стороны равны а и b соответственно)
2) КА = КВ (из условия задачи)
3) КО = КО (так как О является проекцией К на плоскость угла С)
Из этих равенств, мы можем заключить, что треугольники ОАК и ОВК являются равнобедренными.
Теперь, давайте рассмотрим углы этих треугольников. У них есть:
1) Угол ОАК = Угол ОКА (так как треугольник ОАК равнобедренный)
2) Угол ОВК = Угол ОКВ (так как треугольник ОВК равнобедренный)
3) Угол ОКА = Угол ОКВ (так как треугольники ОАК и ОВК базируются на каждой стороне КО)
Теперь имея все эти равенства углов, мы можем заключить, что углы треугольника ОАК равны углам треугольника ОВК. Из этого следует, что треугольники ОАК и ОВК являются подобными (по признаку угол-угол-угол).
Зная, что треугольники ОАК и ОВК являются подобными и имеют равные основания (КА = КВ), мы можем сделать вывод, что их высоты тоже равны. Значит, точки ОА и ОВ лежат на одной горизонтальной линии, что противоречит нашему исходному предположению ОА ≠ ОВ.
2) Теперь давайте рассмотрим второй случай, когда ОА = ОВ.
В этом случае, мы имеем две равные стороны ОА и ОВ, а также равные стороны КА и КВ (из условия задачи).
Зная это, мы можем заключить, что треугольники ОАК и ОВК являются равнобедренными треугольниками (из определения равнобедренного треугольника).
Также, мы знаем, что углы КАО и КВО являются прямыми, так как они образованы перпендикулярными сторонами прямого угла С.
Таким образом, мы можем сделать вывод, что у треугольников ОАК и ОВК равные углы при основании, а также соответственно равные углы при вершине.
Так как, в треугольниках у нас имеются равные стороны и равные углы при основании и вершине, то они полностью равны друг другу.
Окончательно, мы можем заключить, что треугольники ОАК и ОВК равны друг другу.
Теперь давайте рассмотрим четырехугольник ОАСВ. У нас есть:
1) ОА = ОВ (из условия задачи)
2) АС = ВС (сторона угла С)
Поскольку стороны ОА и ОВ равны, а стороны АС и ВС равны, мы можем заключить, что ОАСВ является прямоугольником по определению прямоугольника.
Также, у нас есть следующая информация:
1) Угол ОАС = Угол ОВС (так как углы опираются на равные стороны ОА и ОВ)
2) Угол ОСА = Угол ОСВ (так как углы опираются на равные стороны АС и ВС)
3) Угол ОАС + Угол ОСА = 90 градусов (из определения прямоугольника)
Из этих равенств, мы можем заключить, что все углы четырехугольника ОАСВ являются прямыми углами.
Таким образом, мы доказали, что четырехугольник ОАСВ является квадратом по определению квадрата (имеет равные стороны и прямые углы).
Это и есть доказательство того, что ОАСВ является квадратом.