Рассмотрим произвольный набор целых неотрицательных чисел . Заметим, что каков бы ни был набор , состоящий из нулей и единиц (), сумма имеет одну и ту же четность. Иными словами, если в некоторой сумме поменять знаки нескольких слагаемых, четность суммы от этого не поменяется.
Пойдем по кругу по часовой стрелке и будем складывать разности, причем вычитать будем из следующего (по часовой стрелке) числа. Поскольку мы начали и закончили одним и тем же числом, то итоговая сумма равна нулю. Теперь, если в этой сумме поменять знак отрицательных разностей, то получим сумму модулей из условия. Из замечания в начале следует, что эта сумма четна (поскольку первая сумма равна нулю), однако она равна 4*1+4*2+3*3 - число нечетное, противоречие.
Рассмотрим произвольный набор целых неотрицательных чисел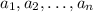
. Заметим, что каков бы ни был набор 
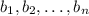, состоящий из нулей и единиц (
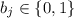), сумма 
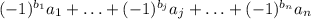имеет одну и ту же четность. Иными словами, если в некоторой сумме поменять знаки нескольких слагаемых, четность суммы от этого не поменяется.
Пойдем по кругу по часовой стрелке и будем складывать разности, причем вычитать будем из следующего (по часовой стрелке) числа. Поскольку мы начали и закончили одним и тем же числом, то итоговая сумма равна нулю. Теперь, если в этой сумме поменять знак отрицательных разностей, то получим сумму модулей из условия. Из замечания в начале следует, что эта сумма четна (поскольку первая сумма равна нулю), однако она равна 4*1+4*2+3*3 - число нечетное, противоречие.
Пошаговое объяснение:
1004.
1) 2,7 - 0,8 = 1,9
2) 1,9 * 2. 1/3 = 1. 9/10 *
2. 1/3 = 19/10 * 7/3 = 133/30
Это числитель дроби
3) 5,2 - 1,4 = 3,8
4) 3,8 : 3/70 = 3. 8/10 : 3/70 = 38/10 : 3/70 = 38/10 * 70/3 = 38/1 * 7/3 = 266/3
Это знаменатель дроби
5) 133/30 : 266/3 =
133/30 * 3/266 = 1/10 * 1/2 = 1/20 = 0,05
Это результат дроби
6) 0,05 + 0,125 = 0,175
Это результат скобки
7) 0,175 : 2. 1/2 =
0,175 : 5/2 = 0,175 : 2,5 =
0,07
8) 0,07 + 0,43 = 0,5
Это результат примера
ответ: 0,5
1005.
1) 2. 3/4 : 1,1 = 11/4 : 1,1 = 2,75 : 1,1 = 2,5
2) 2,5 + 3. 1/3 = 2. 5/10 + 3. 1/3 = 2. 15/30 + 3. 10/30 = 5. 25/30 = 5. 5/6
Это числитель 1 дроби
3) 0,4 * 3. 1/3 = 4/10 * 10/3 = 4/3 = 1. 1/3
4) 2,5 - 1. 1/3 = 2. 5/10 -
1. 1/3 = 2. 15/30 - 1. 10/30 = 1. 5/30 = 1. 1/6
Это знаменатель 1 дроби
5) 5. 5/6 : 1. 1/6 =
35/6 : 7/6 = 35/6 * 6/7 = 35/7 = 5
Это результат 1 дроби
6) 5 : 5/7 = 5 * 7/5 = 1 * 7/1 = 7/1 = 7
7) 2. 1/6 + 4,5 =
2. 1/6 + 4. 5/10 =
2. 5/30 + 4. 15/30 =
6. 20/30 = 6. 2/3
8) 6. 2/3 * 0,375 =
20/3 * 375/1000 = 1/1 * 125/50 = 2,5
Это числитель 2 дроби
9) 2,75 - 1. 1/2 = 2,75 - 3/2 = 2,75 - 1,5 = 1,25
Это знаменатель 2 дроби
10) 2,5 : 1,25 = 2
Это результат 2 дроби
11) 7 - 2 = 5
Это результат всего примера
ответ: 5
1006.
1) 13,75 + 9. 1/6 =
13. 75/100 + 9. 1/6 =
13. 3/4 + 9. 1/6 =
13. 9/12 + 9. 2/12 = 22. 11/12
2) 22. 11/12 * 1,2 =
275/12 * 1. 2/10 =
275/12 * 12/10 = 275/10 = 27,5
Это числитель 1 дроби
3) 10,3 - 8. 1/2 = 10,3 - 17/2 = 10,3 - 8,5 = 1,8
4) 1,8 * 5/9 = 1. 8/10 * 5/9 = 18/10 * 5/9 = 2/2 * 1/1 = 2/2 = 1
Это знаменатель 1 дроби
5) 27,5 : 1 = 27,5
Это результат 1 дроби
6) 6,8 - 3. 3/5 = 6,8 - 18/5 = 6,8 - 3,6 = 3,2
7) 3,2 * 5. 5/6 =
3. 2/10 * 5. 5/6 =
32/10 * 35/6 = 16/2 * 7/3 = 8 * 7/3 = 56/3
Это числитель 2 дроби
8) 3. 2/3 - 3. 1/6 =
3. 4/6 - 3. 1/6 = 3/6 = 1/2
9) 1/2 * 56 = 56/2 = 28
Это знаменатель 2 дроби
10) 56/3 : 28 = 56/3 * 1/28 = 2/3 * 1/1 = 2/3
Это результат 2 дроби
11) 27,5 + 2/3 - 27. 1/6 =
27. 5/10 + 2/3 - 27. 1/6 =
27. 15/30 + 20/30 -
27. 5/30 =
27. 35/30 - 27. 5/30 =
30/30 = 1
Это результат всего примера
ответ: 1