Математика: ть до 7 вечора. Пасіба ть до 7 вечора. Пасіба >

ть до 7 вечора. Пасіба ть до 7 вечора. Пасіба ">

Показать ответ

Ответ:

ghostcatchy

13.09.2021 00:33

Метод сложения, он же метод Гаусса - мой любимый!
{ x + 7y = 19
{ x + 5y = 13
Умножаем 2 уравнение на (-1)
{ x + 7y = 19
{ -x - 5y = -13
Складываем уравнения
2y = 6;
y = 3; x = 13 - 5y = 13 - 5*3 = 13 - 15 = -2
ответ: (-2; 3)

{ 3x - 5y = 23
{ 2x + 3y = 9
Умножаем 1 уравнение на 3, а 2 уравнение на 5
{ 9x - 15y = 69
{ 10x + 15y = 45
Складываем уравнения
19x = 114
x = 114/19 = 6; y = (9 - 2x)/3 = (9 - 2*6)/3 = -3/3 = -1
ответ: (6; -1)

{ 6x + 5y = 0
{ 2x + 3y = -8
Умножаем 2 уравнение на -3
{ 6x + 5y = 0
{ -6x - 9y = 24
Складываем уравнения
-4y = 24
y = -24/4 = -6; x = -5y/6 = -5*(-6)/6 = 5
ответ: (5; -6)

0,0(0 оценок)

Ответ:

Ариана16112001

08.09.2022 23:13

Предположим, что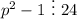 $p^2-1~\vdots ~24$ . Тогда и 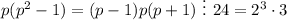$p(p^2-1)=(p-1)p(p+1)~\vdots ~24=2^3\cdot 3$ . Проверим последнее утверждение.

Данное произведение — это произведение трёх последовательных чисел, значит, один из множителей обязательно делится на 3. Так как p простое и больше 3, p-1 и p+1 чётны. Докажем, что произведение p-1 = 2k и p+1 = 2k+2 (k ∈ N) делится на 8:

2k(2k+2)=4k(k+1) . Оно, очевидно, делится на 4. Также оно делится ещё на 2, так как одно из чисел k и k+1 обязательно чётное.

$p(p^2-1)~\vdots~3,~p^2-1~\vdots~8\Rightarrow p(p^2-1)~\vdots~24$ .

Однако из этого не обязательно следует, что и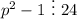 $p^2-1~\vdots~24$ . Но p > 3 и p — простое, значит, p не содержит множителей числа 24, то есть на 24 может делиться только 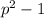p^2-1 , что и требовалось доказать.