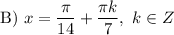Войти Регистрация Спроси ai-bota

Т40) Решите уравнение: tg(4x+π)*tg(3x) = 1

Заранее

Т40) Решите уравнение: tg(4x+π)*tg(3x) = 1Заранее

Показать ответ

Ответ:

miaamkom1

15.10.2020 15:29

$\text{tg}(4x + \pi) \cdot \text{tg} (3x) = 1$

$\text{tg}(4x) \cdot \text{tg} (3x) = 1$

$\dfrac{\sin (4x)}{\cos (4x)} \cdot \dfrac{\sin (3x)}{\cos (3x)} = 1$

$\dfrac{\sin (4x) \sin (3x)}{\cos (4x) \cos (3x)} - 1 = 0$

$\dfrac{\sin (4x) \sin (3x) - \cos (4x) \cos (3x)}{\cos (4x) \cos (3x)} = 0$

$\dfrac{\cos (4x) \cos (3x) - \sin (4x) \sin (3x)}{\cos (4x) \cos (3x)} = 0$

$\dfrac{\cos (7x)}{\cos (4x) \cos (3x)} = 0$

$\left\{\begin{array}{ccc}\cos (7x) = 0\\\cos (4x) \neq 0\\\cos (3x) \neq 0\end{array}\right$

$\left\{\begin{array}{ccc}7x = \dfrac{\pi}{2} + \pi k\\4x \neq \dfrac{\pi}{2} + \pi k\\3x \neq \dfrac{\pi}{2} + \pi k\end{array}\right \ k \in Z$

$\left\{\begin{array}{ccc}x = \dfrac{\pi}{14} + \dfrac{\pi k}{7} \\x \neq \dfrac{\pi}{8} + \dfrac{\pi k}{4} \ \\x \neq \dfrac{\pi}{6} + \dfrac{\pi k}{3} \ \end{array}\right \ k \in Z$

$x = \dfrac{\pi}{14} + \dfrac{\pi k}{7}, \ k \in Z$

ответ: $\text{B}) \ x = \dfrac{\pi}{14} + \dfrac{\pi k}{7}, \ k \in Z$

0,0(0 оценок)

Популярные вопросы: Математика

asiper4ik

12.05.2023 15:14

Выберите числа, в которых отсутствует разряд единиц: 43, 52, 30, 60, 74. Дайте пояснение...

Арте20

17.02.2020 07:07

Сколько было апельсинов если птицы улетели на север в 12:00 а Миша ударил Колю месяц назад на базаре в городе Екатиринбург Африка сколько всего апельсинов было у крыши валеры Евтушенко?...

Mariafetisova1

19.11.2021 07:33

Решите Раскройте скобки! 1) 2/3*( 1 3/4х+5 1/4y-9/10z); 2) 4 4/5*( 2 4/5a-2 1/12в+8 7/30d). Не надо писать что надо просто раскрыть скобки,я всё равно не понимаю. Тут нужно решение!...

Lovetoo

13.03.2021 16:33

Найди значение выражения 9x−7|y−3| при x=−6, y=−3....

kiss86gv

17.09.2022 11:25

Прямокутний трикутник обертається навколо свого катета b= 36 см і навколо свого катета a= 15 см. Визнач бічні поверхні конусів, які утворюються... 1. ...при обертанні навколо довгого...

Vika99000

24.12.2022 20:40

Із 140 кг свіжих вишень отримують 21 кг су- шених. Скільки кілограмів сушених вишень отримають із 160 кг свіжих? Скільки кілограмів свіжих вишень потрібно, щоб отримати 31,5 кг...

anna16191

26.06.2021 02:42

Запишите в видедесятичных дробей смешанные числа...

ghjcvsdhcs

14.05.2022 12:07

28. занимаются в макружке?Из лагеря вышли пять туристов: Берик, Баян, Ерлан, Карлыгаш, Зульфия. Ерланидет впереди Зульфии,Карлыгаш – впереди Берика, но позади Зульфии, Баян- впередиЕрлана....

mariooouvanov

30.06.2022 20:44

Зависимость между объёмом стали и его массоймпрямо пропорциональна.Масса стали объёмом 12 см³ равна 15,6 г 1)Какова массастали объемом 12 см³? 2) Какому объёму соответствует сталь...

yulakri

27.04.2022 05:22

Шесть бобров построили платину за 6 дней. весной платину смыло.тогда бобры позвали соседей и за 3 дня снова построили плотину в 2 раза выше . сколько позвали бобры?...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку