Там написано нода найти неизвестный член пропорции​

ответы в объяснении

Пошаговое объяснение:

Вспомним нужные сведения:

1) Уравнение окружности с центром в точке О(x0; y0) и радиусом r имеет вид: (x-x0)²+(y-y0)²=r².

2) Расстояние от точки T(x1; y1) до точки P(x2; y2) определяется по формуле: .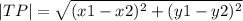

Решение задачи.

Найдем расстояние |FD| и |BD| :

Дана окружность с центром в точке А(3; 4) и радиусом r²=9. Тогда уравнение окружности имеет вид:

(x-3)²+(y-4)²=9

Теперь определим, какие точки лежат на окружности а какие нет. Если точка лежит на окружности, то её координаты удовлетворяют уравнение окружности.

А(3;4) : (3-3)²+(4-4)²=0 ≠ 9 , не лежит на окружности!

B(3;7) : (3-3)²+(7-4)²=9 = 9 , лежит на окружности!

F(0;4) : (0-3)²+(4-4)²=9 = 9 , лежит на окружности!

D(3;1) : (3-3)²+(1-4)²=9 = 9 , лежит на окружности!

E(6;4) : (6-3)²+(4-4)²=9 = 9 , лежит на окружности!

M(6;7) : (6-3)²+(7-4)²=18 ≠ 9 , не лежит на окружности!

Теперь определим расстояние от начала координат до центра окружности. Координаты начала координат О(0; 0), а координаты центра окружности А(3; 4):

1/3

Пошаговое объяснение:

Рассмотрим два события и вычислим их вероятности:

1) Первым был вынут черный шар, вторым белый.

Первым был вынут черный шар с вероятностью 24/(12+24)=2/3.

Осталось 12 белых и 23 черных шара. Вероятность того, что был вынут белый шар, равна 12/(12+23)=12/35.

Вероятность, что сначала вынули черный шар, а потом белый, равна (2/3)*(12/35)=8/35

2) Первым был вынут белый шар, вторым тоже белый.

Первым был вынут белый шар с вероятностью 12/(12+24)=1/3.

Осталось 11 белых и 24 черных шара. Вероятность того, что был вынут белый шар, равна 11/(11+24)=11/35.

Вероятность, что сначала вынули черный шар, а потом белый, равна (1/3)*(11/35)=11/105

Значит, вероятность того, что вторым по счету вынули белый шар, составляет 8/35+11/105=35/105=1/3