Можно, конечно, начертить графики и увидеть, что пересечений нет, но я напишу более строгое доказательство.
Чтобы уравнение имело решения, нужно чтобы область значений функции включала в себя ноль.
Найдем область значений функции . Для этого найдем точки экстремума.
Так как при x < 0 y' < 0, а при x > 0 y' > 0, то x = 0 - точка минимума, в ней достигается наименьшее значение функции. Найдем его: для этого ноль необходимо подставить в исходную функцию.
y(0) = e⁰ - 0 = 1 - 0 = 1 > 0.
Уже сразу видно, что уравнение не имеет решений, т.к. если минимум функции больше 0, то понятно, что и любое другое значение функции тоже больше 0, а значит значение функции никогда не может равняться нулю и равенство выполняться не может, т.е. уравнения не имеет решений.
Пошаговое объяснение:
1) pi/4+2pi*n<= x<= 7/4pi+2pi*n, где n принадлежит Z
2)-3pi/4+2pi*n<= x<= 3/4pi+2pi*n, где n принадлежит Z
3) -pi/6+2pi*n<= x<= 7/6pi+2pi*n, где n принадлежит Z
4) pi/6+2pi*n<= x<= 5/6pi+2pi*n, где n принадлежит Z
5) -pi/4+2pi*n<= x<= pi/4+2pi*n, где n принадлежит Z
6) -pi/6+2pi*n<= x<= pi/6+2pi*n, где n принадлежит Z
7) -5/6pi+2pi*n<= x<= 5/6pi+2pi*n, где n принадлежит Z
8) -7/6pi+2pi*n<= x<= pi/6+2pi*n, где n принадлежит Z
9) -5/6pi+2pi*n<= x<= -pi/6+2pi*n, где n принадлежит Z
10) 2pi*n, т.к. область значений cos и sin [-1;1]
11) (-беск;+беск)
12) pi/3+2pi*n<= x<= 2/3pi+2pi*n, где n принадлежит Z
13)-3pi/4+2pi*n<= x<= 3/4pi+2pi*n, где n принадлежит Z
Я Вам все не могу объяснить,много писать,но если хотите разобраться, то вот сайт https://egemaximum.ru/prostejshie-trigonometricheskie-neravenstva/
Можно, конечно, начертить графики и увидеть, что пересечений нет, но я напишу более строгое доказательство.
Чтобы уравнение имело решения, нужно чтобы область значений функции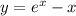
включала в себя ноль.
Найдем область значений функции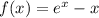
. Для этого найдем точки экстремума.
Так как при x < 0 y' < 0, а при x > 0 y' > 0, то x = 0 - точка минимума, в ней достигается наименьшее значение функции. Найдем его: для этого ноль необходимо подставить в исходную функцию.
y(0) = e⁰ - 0 = 1 - 0 = 1 > 0.
Уже сразу видно, что уравнение не имеет решений, т.к. если минимум функции больше 0, то понятно, что и любое другое значение функции тоже больше 0, а значит значение функции никогда не может равняться нулю и равенство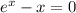
выполняться не может, т.е. уравнения 
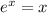не имеет решений.
ОТВЕТ: 0.