Тарас зібрав 45 грибів а яких 2/9 становили білі.Скільки білих грибів зібрав Tарас

Показать ответ

Ответ:

iskanderkhusano

30.05.2023 06:22

Пошаговое объяснение:

Спросим бога B: «Если я с у тебя „Бог А — бог случая?“, ты ответишь „ja“?». Если бог B отвечает «ja», значит, либо он бог случая (и отвечает случайным образом), либо он не бог случая, а на самом деле бог A — бог случая. В любом варианте, бог C — это не бог случая. Если же B отвечает «da», то либо он бог случая (и отвечает случайным образом), либо B не бог случая, что означает, что бог А — тоже не бог случая. В любом варианте, бог A — это не бог случая.

Спросим у бога, который не является богом случая (по результатам предыдущего вопроса, либо A, либо C): «Если я с у тебя: „ты - бог лжи?“, ты ответишь „ja“?». Поскольку он не бог случая, ответ «da» обозначает, что он бог правды, а ответ «ja» обозначает, что он бог лжи.

Спросим у этого же бога «Если я у тебя с : „Бог B — бог случая?“, ответишь ли ты „ja“?». Если ответ «ja» — бог B является богом случая, если ответ «da», то бог, с которым ещё не говорили, является богом случая.

Оставшийся бог определяется методом исключения.

0,0(0 оценок)

Ответ:

olyamin0

22.03.2020 03:59

$15 \sqrt{1.04} - \frac{3}{4} \sqrt{5 \frac{5}{9} } + 2 \sqrt{ \frac{1}{18} } - (5 \sqrt{0.02} - \sqrt{300} ) = 3 \sqrt{26} - \frac{17}{12} \sqrt{2} + 10 \sqrt{3}$

$15 \sqrt{1.04} - \frac{3}{4} \sqrt{5 \frac{5}{9} } + 2 \sqrt{ \frac{1}{18} } - (5 \sqrt{0.02} - \sqrt{300} ) =...$

Свойства квадратных корней, которыми воспользуемся:

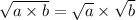1) $\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}$ ;

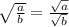2) $\sqrt{ \frac{a}{b} } = \frac{ \sqrt{a} }{ \sqrt{b} }$ ;

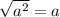3) $\sqrt{ {a}^{2} } = a$ .

Итак, для начала нужно разложить числа под корнем на множители. Причём на такие множители, которые являются квадратом какого-то числа, чтобы можно было воспользоваться третьим свойством корней и вынести из под знака корня это какое-то число, тем самым упростить.

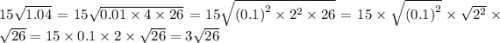1) $15 \sqrt{1.04} = 15 \sqrt{0.01 \times 4 \times 26} = 15 \sqrt{ {(0.1)}^{2} \times {2}^{2} \times 26 } = 15 \times \sqrt{ {(0.1)}^{2} } \times \sqrt{ {2}^{2} } \times \sqrt{26} = 15 \times 0.1 \times 2 \times \sqrt{26} = 3 \sqrt{26}$ ;

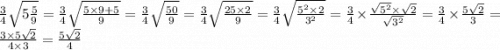2) $\frac{3}{4} \sqrt{5 \frac{5}{9} } = \frac{3}{4} \sqrt{ \frac{5 \times 9 + 5}{9} } = \frac{3}{4} \sqrt{ \frac{50}{9} } = \frac{3}{4} \sqrt{ \frac{25 \times 2}{9} } = \frac{3}{4} \sqrt{ \frac{ {5}^{2} \times 2 }{ {3}^{2} } } = \frac{3}{4} \times \frac{ \sqrt{ {5}^{2} } \times \sqrt{2} }{ \sqrt{ {3}^{2} } } = \frac{3}{4} \times \frac{5 \sqrt{2} }{3} = \frac{3 \times 5 \sqrt{2} }{4 \times 3} = \frac{5 \sqrt{2} }{4}$ ;

3) $2 \sqrt{ \frac{1}{18} } = 2 \sqrt{ \frac{1}{9 \times 2} } = 2 \sqrt{ \frac{1}{ {3}^{2} \times 2} } = 2 \times \frac{ \sqrt{1} }{ \sqrt{ {3}^{2} } \times \sqrt{2} } = 2 \times \frac{1}{3 \sqrt{2} } = \frac{2}{3 \sqrt{2} } =...$

для удобства дальнейшего решения избавимся от иррациональности в знаменателе, то есть, от знака корня в знаменателе

$... = \frac{2}{3 \sqrt{2} } \times \frac{ \sqrt{2} }{ \sqrt{2} } = \frac{2 \sqrt{2} }{3 \times \sqrt{2} \times \sqrt{2} } = \frac{2 \sqrt{2} }{3 \times 2} = \frac{ \sqrt{2} }{3}$ ;

4) $5 \sqrt{0.02} = 5 \sqrt{0.01 \times 2} = 5 \sqrt{ {(0.1)}^{2} \times 2} = 5 \times \sqrt{ {(0.1)}^{2} } \times \sqrt{2} = 5 \times 0.1 \times \sqrt{2} = 0.5 \times \sqrt{2} = \frac{5}{10} \times \sqrt{2} = \frac{1}{2} \times \sqrt{2} = \frac{ \sqrt{2} }{2}$ ;

5) $\sqrt{300} = \sqrt{100 \times 3} = \sqrt{ {10}^{2} \times 3} = \sqrt{ {10}^{2} } \times \sqrt{3} = 10 \sqrt{3}$

Теперь объединяем это всё:

$... = 3 \sqrt{26} - \frac{5 \sqrt{2} }{4} + \frac{ \sqrt{2} }{3} - ( \frac{ \sqrt{2} }{2} - 10 \sqrt{3} ) = 3 \sqrt{26} - \frac{5 \sqrt{2} }{4} + \frac{ \sqrt{2} }{3} - \frac{ \sqrt{2} }{2} + 10 \sqrt{3} = ...$

Сгруппируем числа с разными корнями:

$... = 3 \sqrt{26} - ( \frac{5 \sqrt{2} }{4} - \frac{ \sqrt{2} }{3} + \frac{ \sqrt{2} }{2} ) + 10 \sqrt{3} = 3 \sqrt{26} - ( \frac{5 \sqrt{2} \times 3}{12} - \frac{ \sqrt{2} \times 4}{12} + \frac{ \sqrt{2} \times 6 }{12} ) + 10 \sqrt{3} = 3 \sqrt{26} - ( \frac{15 \sqrt{2} - 4 \sqrt{2} + 6 \sqrt{2} }{12} ) + 10 \sqrt{3} = 3 \sqrt{26} - ( \frac{ \sqrt{2} (15 - 4 + 6)}{12} ) + 10 \sqrt{3} = 3 \sqrt{26} - \frac{17 \sqrt{2} }{12} + 10 \sqrt{3} = 3 \sqrt{26} - \frac{17}{12} \sqrt{2} + 10 \sqrt{3}$