Возможно, Вы ошиблись с длиной одной из сторон ( в других задачах они равны 7 см и 16 см, у Вас 7 см и 16 миллиметров), но для решения задачи это несущественно.
Очень подробно :
Треугольник можно определить как замкнутую ломаную линию из трёх звеньев, и эти звенья не лежат на одной прямой.
Если сумма длин двух звеньев равна длине третьего звена, треугольник не получится, т.к. меньшие звенья "лягут" на большее звено, хотя их концы и соединятся.
Если сумма длин меньших звеньев меньше длины большего звена, эти звенья "лягут на большее и их концы не достанут друг до друга.
*************
Пусть третья сторона будет а.
Тогда а<(70 +16,) т.е. а< 86 мм ( или 8, 6 см)
Отсюда же следует. что .70< а+16
И
а>70-16 , т.е. а>54 мм ( или 5, 4 см)
Из этого следует неравенство треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон и больше их разности. 54 мм < a < 86 мм
---------
Объяснение дано упрощенно. Доказательство теоремы о неравенстве треугольника есть в учебнике.
Возможно, Вы ошиблись с длиной одной из сторон ( в других задачах они равны 7 см и 16 см, у Вас 7 см и 16 миллиметров), но для решения задачи это несущественно.
Очень подробно :
Треугольник можно определить как замкнутую ломаную линию из трёх звеньев, и эти звенья не лежат на одной прямой.
Если сумма длин двух звеньев равна длине третьего звена, треугольник не получится, т.к. меньшие звенья "лягут" на большее звено, хотя их концы и соединятся.
Если сумма длин меньших звеньев меньше длины большего звена, эти звенья "лягут на большее и их концы не достанут друг до друга.
*************
Пусть третья сторона будет а.
Тогда а<(70 +16,) т.е. а< 86 мм ( или 8, 6 см)
Отсюда же следует. что .70< а+16
И
а>70-16 , т.е. а>54 мм ( или 5, 4 см)
Из этого следует неравенство треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон и больше их разности. 54 мм < a < 86 мм
---------
Объяснение дано упрощенно. Доказательство теоремы о неравенстве треугольника есть в учебнике.
Всего 8 различных таких троек.
Пошаговое объяснение:
Итак, известно: 3 числа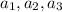
такие, что:
Найти: число возможных вариантов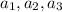
Решение: т.к. все 3 числа - члены геом. прогрессии, запишем так:
Теперь преобразуем полученное равенство:
Сделаем замену:
Получили произведение 2 множителей, про которые известно, что а1 - натуральное, k - целое..
т.к. а1 - натуральное, 147 - натуральное =>
=> и значение t тоже должно быть натуральным числом.
И, очевидно, значение а1 и t ограничено сочетаниями множителей, на которые можно разложить 147.
Разложим:
147 = 1•3•7•7
Итак, как а, так и t могут принимать значения из множества: {1; 3; 7; 21; 49; 147}
Рассмотрим t. обратная замена;
График t(k)= k²+k+1 - парабола, с вершиной в точке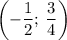
, ветви вверх.
При значениях t = 49; t = 147 k - не является целым числом, так что они для t не подойдут
Итак: Всего возможно 8 различных значений для k
И для каждого варианта k существует единственный вариант значения а1.
То есть - следовательно, всего различных наборов чисел может быть столько же, сколько различных значений k.
Т. е. всего 8 вариантов различных троек чисел