Теория вероятности
непрерывная случайная величина задана дифференциальной функцией
найти: а) параметр а
б) интегральную функцию распределения f(x)
в) ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану и асимметрию
г) p(1< =x< =2). построить графики f(x) и f(x). изобразить вероятность p(1< =x< =2)

1)210|2           98|2

    105|3           49|7

    35   |5           7|7

      7   |7           1 |

      1   |

нод(210,98)=2*7=14

нок (210,98)=2*7*3*5*7=1470

1470: 14=105

ответ: в 105 раз

2) 1. 3-1/9=2 9/9-1/9=2 8/9 (ч)- лодка плыла по течению

    2. 46: 2 8/9= 46 : 26/9=15   12/13 (км/ч)-по течению

    3. 15   12/13 - 1   3/4 = 14   9/52 (км/ч) в стоячей воде

    4. 14   9/52 * 2 = 28   9/26 (км) в стоячей воде

1. б) (-3; 8]

2. а)

3. x∈ [-1; 2)

4. x∈ (-3; +∞)

5. x∈ (-1,5; 6]

6. x∈ [1/5; 2]

7. x∈ (-∞; 12]

8. x∈ [-2; 3]

Пошаговое объяснение:

1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]

2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.

3.

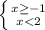
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)

4.

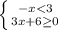
Отсюда x>-3 или x∈ (-3; +∞)

5. -6 ≤ 6-2x < 9

-6-6 ≤ -2x < 9-6

-12 ≤ -2x < 3

-12:(-2) ≥ x > 3:(-2)

-1,5 < x ≤ 6 или x∈ (-1,5; 6]

6. При каких значениях переменной имеет смысл выражение

Данное выражение имеет смысл, если подкоренные выражения не отрицательные:

1/5 ≤ x ≤ 2 или x∈ [1/5; 2]

7. Решите совокупность неравенств

Отсюда  х ≤ 12 или x∈ (-∞; 12]

8.

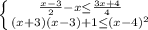
Отсюда  -2 ≤ х ≤ 3 или x∈ [-2; 3]