Рассмотрим последовательность k-эй член которой определяется так:
причем это число неотрицательно, и меньше s. Проще говоря, это остаток от деления 10^n на s. Ясно, что последовательность периодична и ее период не больше s. Обозначим ее период t.
Теперь рассмотрим число записанное последовательностью цифр . То есть число
Очевидно, что
Возьмем такое число , что , для и во всех остальных случаях. Иными словами возьмем число которое стоит из s периодических блоков состоящих из нуля и одной единицы в конце.
Тогда наше число будет состоять из s единиц и какого-то кол-ва нулей. В этом случае, сумма цифра числа s, как и требовалось. Также
Таким образом, оба требуемых условия оказались удовлетворены.
Приведенное выше рассуждение не проходит, если s делится на какую-то степень 10, т. е. оканчивается N нулями. В этом случае построим число n для , только возьмем блоков , а не . После этого припишем к результату N нулей. Ясно, что и в этом случае число построено верно.
Рассмотрим последовательность k-эй член которой определяется так:
причем это число неотрицательно, и меньше s. Проще говоря, это остаток от деления 10^n на s. Ясно, что последовательность периодична и ее период не больше s. Обозначим ее период t.
Теперь рассмотрим число записанное последовательностью цифр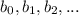 . То есть число
. То есть число
Очевидно, что
Возьмем такое число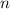 , что
, что 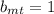 , для
, для 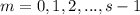 и
и 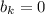 во всех остальных случаях. Иными словами возьмем число которое стоит из s периодических блоков состоящих из
во всех остальных случаях. Иными словами возьмем число которое стоит из s периодических блоков состоящих из 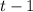 нуля и одной единицы в конце.
нуля и одной единицы в конце.
Тогда наше число будет состоять из s единиц и какого-то кол-ва нулей. В этом случае, сумма цифра числа s, как и требовалось. Также
Таким образом, оба требуемых условия оказались удовлетворены.
Приведенное выше рассуждение не проходит, если s делится на какую-то степень 10, т. е. оканчивается N нулями. В этом случае построим число n для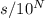 , только возьмем блоков
, только возьмем блоков  , а не
, а не 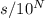 . После этого припишем к результату N нулей. Ясно, что и в этом случае число построено верно.
. После этого припишем к результату N нулей. Ясно, что и в этом случае число построено верно.
Пошаговое объяснение:
Р(2,5² - 1,5²) = (1 * 4) = (4) - координата Р
Н((2,5+1,5)/2) = (2) - координата Н
РQ = HQ
|4 - Q| = |2 - Q|
1) Q < 2
4 - Q = 2 - Q
4 = 2 - нет решений
2) 2 < Q < 4
4 - Q = Q -2
2Q = 6
Q = 3
3) Q > 4
Q - 4 = Q - 2
4 = 2 - не верно
нет решений
значит, Q(3)
(0)___(1)___H(2)___Q(3)___P(4)>
7.
от противного
пусть все мальчики собрали разное количество орехов
тогда минимальное количество орехов, которое они могли собрать:
0 + 1 + 2 + ... + 14 = 14*15/2 = 7 * 15 = 105 > 100
противоречие, значит, не могли все собрать разное количество орехов, а значит, найдутся минимум два мальчика, набравшие одинаковое количество орехов
Доказано.