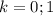Пусть время первого х часов , второго у часов. Тогда производительность первого 1/x, второго 1/y. Вместе они работали 3 целых 3/5 часа = 18/5. Значит, совместная производительность 5/18. Первое уравнение 1/х + 1/у = 5/18
Второй сделал 1/3 работы за 1/3 : 1/у = у/3, первый сделал оставшуюся часть 2/3 работы зв 2/3 : 1/х =2х/3. Всего они работали 8 часов. Второе уравнение
2х/3 + у/3 = 8. Получили систему. Из первого уравнения 18x+18y=5xy, из второго
2x+y = 24. Отсюда, у = 24-2х. Подставим в первое, после упрощения получим:
5x^2 -69 +216 = 0, x=9, тогда у=24-18=6, т.е. время первого 9 часов, второго 6 часов
Или х=4,8 тогда у=14,4, т.е время первого 4,8 часа, второго 14,4 часа
Тогда комплексно-сопряженное числу комплексному числу :
-------(2)
( то же что у вас z с чертой!)
а)
б) Запишем наше комплексное число в тригонометрической форме:
--------(1)
где модуль комплексного числа
В нашем случае
---------(2)
Итак, число в тригонометрической форме с учетом (1) и (2):
Для нахождения четвертой степени числа применим формулу Муавра при :
Известно, что корень n-й степени из комплексного значения имеет n различных значений. В нашем случае нужно найти корень 2-й степени, а значит корень 2-й принимает два различных значения.
Пусть время первого х часов , второго у часов. Тогда производительность первого 1/x, второго 1/y. Вместе они работали 3 целых 3/5 часа = 18/5. Значит, совместная производительность 5/18. Первое уравнение 1/х + 1/у = 5/18
Второй сделал 1/3 работы за 1/3 : 1/у = у/3, первый сделал оставшуюся часть 2/3 работы зв 2/3 : 1/х =2х/3. Всего они работали 8 часов. Второе уравнение
2х/3 + у/3 = 8. Получили систему. Из первого уравнения 18x+18y=5xy, из второго
2x+y = 24. Отсюда, у = 24-2х. Подставим в первое, после упрощения получим:
5x^2 -69 +216 = 0, x=9, тогда у=24-18=6, т.е. время первого 9 часов, второго 6 часов
Или х=4,8 тогда у=14,4, т.е время первого 4,8 часа, второго 14,4 часа
Дано комплексное число в алгебраической форм:
в алгебраической форм:
где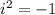 по определению
по определению
Тогда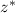 комплексно-сопряженное числу комплексному числу
комплексно-сопряженное числу комплексному числу  :
:
(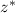 то же что у вас z с чертой!)
то же что у вас z с чертой!)
а)
б) Запишем наше комплексное число в тригонометрической форме:
в тригонометрической форме:
где модуль комплексного числа
модуль комплексного числа 
В нашем случае
Итак, число в тригонометрической форме с учетом (1) и (2):
в тригонометрической форме с учетом (1) и (2):
Для нахождения четвертой степени числа применим формулу Муавра при
применим формулу Муавра при 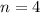 :
:
Известно, что корень n-й степени из комплексного значения имеет n различных значений. В нашем случае нужно найти корень 2-й степени, а значит корень 2-й принимает два различных значения.
при