Обратим внимание, что все четные числа из указанного ряда, кроме четвёрки, имеют в качестве делителя двойку максимум в первой степени, а значит, данные числа вторично не разделятся нацело на два. Эти четные числа нельзя разложить на произведение двух различных чисел одинаковой четности: для них будет иметь место разложение вида N = 2*(нечетное число), какое не представимо в виде разности квадратов x² - y² = (x - y)·(x + y), /где x и у - натуральные числа/,
поскольку соотношение (x - y)·(x + y) = 2*q не решается в целых числах: , где q - нечетное число. Решением системы является пара
х = (q/2) + 1, y = (q/2) - 1, при нечетном q не удовлетворяющая условию:
х ∈ Z, y ∈ Z ⇒ числа 2; 6; 10; 14; 18; 22; 26; 30; 34; 38; 42; 46; 50; 54; 58; 62; 66; 70; 74; 78; 82; 86; 90; 94; 98 невозможно записать как x² - y².
Единицу тоже нельзя записать таким образом, ибо ноль не относится
к натуральным числам, он - число целое. Четверка также не даёт разбиение на два различных множителя одинаковой четности, поэтому как разность квадратов x² - y² её представить нельзя.
Делим 100 на 2 - получаем 50. То есть 50 чисел которые не делятся на два. Найдем сколько чисел из 50 делятся на 3, то есть разделим 50 на 3. Получается 16,6, то есть примерно 17. Значит 17 чисел из 50 делятся на три, остальные - нет. 50 минус 17 будет 33.
Также можно просто проверить перебором. Сразу запишем все нечетные числа от 1 до 100 так как они не делятся на 2. 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 Из них уберем те, что делятся на 3. 1 5 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 83 85 89 91 95 97 И теперь просто посчитаем что осталось. Получим 33.
Положительные целые числа меньше 101, отвечающие заданному условию: 1; 2; 4; 6; 10; 14; 18; 22; 26; 30; 34; 38; 42; 46; 50; 54; 58; 62; 66;
70; 74; 78; 82; 86; 90; 94; 98 – всего 27 чисел.
Обратим внимание, что все четные числа из указанного ряда, кроме четвёрки, имеют в качестве делителя двойку максимум в первой степени, а значит, данные числа вторично не разделятся нацело на два. Эти четные числа нельзя разложить на произведение двух различных чисел одинаковой четности: для них будет иметь место разложение вида N = 2*(нечетное число), какое не представимо в виде разности квадратов x² - y² = (x - y)·(x + y), /где x и у - натуральные числа/,
поскольку соотношение (x - y)·(x + y) = 2*q не решается в целых числах: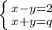
, где q - нечетное число. Решением системы является пара
х = (q/2) + 1, y = (q/2) - 1, при нечетном q не удовлетворяющая условию:
х ∈ Z, y ∈ Z ⇒ числа 2; 6; 10; 14; 18; 22; 26; 30; 34; 38; 42; 46; 50; 54; 58; 62; 66; 70; 74; 78; 82; 86; 90; 94; 98 невозможно записать как x² - y².
Единицу тоже нельзя записать таким образом, ибо ноль не относится
к натуральным числам, он - число целое. Четверка также не даёт разбиение на два различных множителя одинаковой четности, поэтому как разность квадратов x² - y² её представить нельзя.
Найдем сколько чисел из 50 делятся на 3, то есть разделим 50 на 3. Получается 16,6, то есть примерно 17. Значит 17 чисел из 50 делятся на три, остальные - нет. 50 минус 17 будет 33.
Также можно просто проверить перебором. Сразу запишем все нечетные числа от 1 до 100 так как они не делятся на 2.
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99
Из них уберем те, что делятся на 3.
1 5 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 83 85 89 91 95 97
И теперь просто посчитаем что осталось. Получим 33.