Числители образуют следующую последовательность: для соседних натуральных чисел и между ними выписываются натуральные от до .
Для знаменателей наоборот: от до .
Числители.
Рассмотрим множество номеров, под которыми стоит число 2020. Для этого разобьем числа на блоки. Длина каждого блока под номером равна . Для всех блоков с номером число 2020 появляться не будет. Начиная с число 2020 будет в каждом блоке ровно 1 раз (числа в блоках различны). Первый раз число 2020 появится на месте. Затем 2020 будет в каждом блоке под номером . Значит, множество мест числа 2020 задано последовательностью .
Знаменатели.
Число 2019 впервые появится в блоке . Далее будет в каждом блоке под номером 2019. Значит, множество мест число 2019 задано последовательностью . Мы ищем число , поэтому . Следовательно, это число будет стоят на месте под номером
Числители образуют следующую последовательность: для соседних натуральных чисел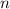 и
и 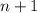 между ними выписываются натуральные от
между ними выписываются натуральные от  до
до  .
.
Для знаменателей наоборот: от до
до  .
.
Числители.
Рассмотрим множество номеров, под которыми стоит число 2020. Для этого разобьем числа на блоки. Длина каждого блока под номером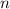 равна
равна 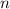 . Для всех блоков с номером
. Для всех блоков с номером 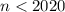 число 2020 появляться не будет. Начиная с
число 2020 появляться не будет. Начиная с 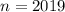 число 2020 будет в каждом блоке ровно 1 раз (числа в блоках различны). Первый раз число 2020 появится на
число 2020 будет в каждом блоке ровно 1 раз (числа в блоках различны). Первый раз число 2020 появится на 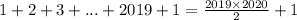 месте. Затем 2020 будет в каждом блоке
месте. Затем 2020 будет в каждом блоке 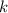 под номером
под номером 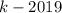 . Значит, множество мест числа 2020 задано последовательностью
. Значит, множество мест числа 2020 задано последовательностью 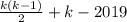 .
.
Знаменатели.
Число 2019 впервые появится в блоке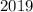 . Далее будет в каждом блоке под номером 2019. Значит, множество мест число 2019 задано последовательностью
. Далее будет в каждом блоке под номером 2019. Значит, множество мест число 2019 задано последовательностью 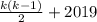 . Мы ищем число
. Мы ищем число 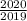 , поэтому
, поэтому 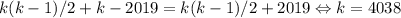 . Следовательно, это число будет стоят на месте под номером
. Следовательно, это число будет стоят на месте под номером 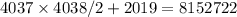
20
Пошаговое объяснение:
Пусть дана арифметическая прогрессия:
Сумма ее n-членов:
Формула n-го члена:
По условию:
Также по условию:
Полученные уравнения запишем в систему:
Вычтем из первого уравнения второе, тогда получится:
3nd-60d=0
3d(n-20)=0
3d=0 или n-20=0
d=0 или n=20
Если d=0, тогда n может быть любым натуральным число. Либо n=20.
Проверим d=0:
Поставляем в уравнение 2a₁+nd-22d=0 корень d=0, тогда
2a₁=0 ⇒ a₁=0, тогда
И наше первое условие запишется как:
Так как на 0 делить нельзя, значит d=0 нам не подходит и остается ответ с фиксированным значением n=20