Точки А (3;-4;7) и В (-5;6;-3) симметричны относительно точки О. Найдите ее координаты

Показать ответ

Ответ:

Нурсултан05072017

15.12.2022 20:15

а) ошибки не будут обнаружены; вероятность = 1/30

б) будет обнаружена хотя бы одна ошибка вероятность = 29/30

Пошаговое объяснение:

Наше событие

А = {из 6 выбранных отчетов хотя бы одна ошибка }

Противоположное событие

$\overline A$ = { из 6 выбранных отчетов ни одной ошибки} =

= {все 6 отчетов верные} =

= { ошибки не будут обнаружены }

Запишем вероятность события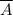 $\overline A$ по формуле классического определения вероятности.

Общее число исходов

$\displaystyle n= C_{10}^6=\frac{10!}{6!(10-6)!} =\frac{7*8*9*10}{2*3*4} =210$

Благоприятное число исходов (выбрать 6 правильных отчетов из 7 правильных)

$\displaystyle n= C_{7}^6=\frac{7!}{6!(7-6)!} =7$

Таким образом вероятность того, что все 6 отчетов будут верные, т.е.

а) ошибки не будут обнаружены

$\displaystyle P(\overline A)= \frac{7}{210} =\frac{1}{30}$

б) будет обнаружена хотя бы одна ошибка

$\displaystyle P(A) = 1-P(\overline A)=1-\frac{1}{30} =\frac{29}{30}$

#SPJ1

0,0(0 оценок)

Ответ:

NikoBellic99

25.02.2020 23:09

371

Пошаговое объяснение:

Комиссия должна состоять из 6-ти человек - немцев и русских. В состав комиссии должно войти не менее 2 немцев, т.е. там может быть 2 немца и 4 русских ИЛИ 3 немца и 3 русских ИЛИ 4 немца и 2 русских. Союз "ИЛИ" - заменяем сложением.

Количество выбрать двух немцев из четырех - это количество сочетаний из 4 по 2, т.к. порядок выбора неважен. Количество выбрать четырёх русских из семи - это количество сочетаний из 7 по 4, т.к. порядок выбора неважен. Полученное количество сочетаний перемножаем.

Точно так же поступаем дальше, выбирая трёх немцев из четырех и трех русских из семи, а также выбирая четырех немцев из четырех и двух русских из семи.

Запись решения:

$C_4^2*C_7^4+C_4^3*C_7^3+C_4^4*C_7^2=\frac{4!}{2!2!}*\frac{7!}{4!3!}+\frac{4!}{3!1!}*\frac{7!}{3!4!}+1*\frac{7!}{2!5!}==5*6*7+4*5*7+3*7=7*(30+20+3)=371$