Пусть первая прямая имеет угловой коэффициент , а вторая прямая имеет угловой коэффициент , где и - соответствующие углы наклона прямых к положительному направлению оси .
Рассмотрим угол между этими прямыми. Пусть , тогда он равен . Найдем соотношение между этим углом и угловыми коэффициентами прямых. Используем формулу тангенса разности:
Так как мы хотим получить условие перпендикулярности двух прямых, то считаем угол между прямыми .
Тангенс 90 градусов не определен, но можно сказать что он стремится к бесконечности к стремлении аргумента к 90 градусам.
Но если дробь стремится к бесконечности, то знаменатель стремится к нулю.
В пределе знаменатель равен нулю. Тогда получим:
Можно выразить один из коэффициентов:
Тогда формулируется легкое правило: Две прямые перпендикулярны, когда их угловые коэффициенты являются противоположными обратными числами.
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
Составим характеристическое уравнение и решим его:
Общее решение однородного уравнения:
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
Пусть первая прямая имеет угловой коэффициент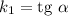
, а вторая прямая имеет угловой коэффициент 
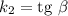, где 
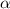и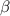 
- соответствующие углы наклона прямых к положительному направлению оси 
.
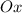Рассмотрим угол между этими прямыми. Пусть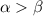
, тогда он равен 
. Найдем соотношение между этим углом и угловыми коэффициентами прямых. Используем формулу тангенса разности:
Так как мы хотим получить условие перпендикулярности двух прямых, то считаем угол между прямыми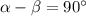
.
Тангенс 90 градусов не определен, но можно сказать что он стремится к бесконечности к стремлении аргумента к 90 градусам.
Но если дробь стремится к бесконечности, то знаменатель стремится к нулю.
В пределе знаменатель равен нулю. Тогда получим:
Можно выразить один из коэффициентов:
Тогда формулируется легкое правило: Две прямые перпендикулярны, когда их угловые коэффициенты являются противоположными обратными числами.
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
Составим однородное дифференциальное уравнение, соответствующее данному неоднородному:
Составим характеристическое уравнение и решим его:
Общее решение однородного уравнения:
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
Находим первую производную:
Находим вторую производную:
Подставляем в исходное уравнение:
Условие равенства левой и правой частей:
Частное решение данного неоднородного уравнения:
Общее решение данного неоднородного уравнения: