По условию характеристические многочлены матриц второго порядка А и В совпадают. Поскольку характеристический многочлен ищется по формуле
делаем вывод, что
Если бы корни характеристического уравнения были бы разные, все матрицы с таким характеристическим уравнением были бы подобны, то есть были бы матрицами одного и того же оператора. Но по условию это не так. Вывод: а матрицы второго порядка с таким условием бывают двух видов: - скалярная матрица (а поскольку по условию след равен 10, это скалярная матрица 5E, где E - единичная матрица), и те, которые подобны жордановой клетке с пятерками на диагонали. Поскольку определитель матрицы (как и ее след) не зависят от выбора базиса, делаем вывод, что определители матриц А и В равны 25.
ответ:
Замечание. Зачем было путать потенциальных "решателей" и писать в условии AA и BB вместо А и В? Не понимаю.
Замечание. Tr A - это обозначение для следа матрицы, то есть суммы элементов, стоящих на главной диагонали, det A - обозначение для определителя матрицы.
Если подбором, то можно мыслить так: число рублей у Оли должно делиться без остатка на 4 и быть меньше 15. Поэтому у нее може быть 4 рубля, или 8 рублей, или 12 рублей. Подбираем: 1) если 4 рубля, то тогда карандаш стоит 4 :4 = 1 рубль, а альбом 4 рубля. 4 + 1 не равно 15. Значит, не подходит. 2) Если 8 рублей, то тогда карандаш стоит 8 : 4 = 2 рубля, а альбом 8 рублей. 8 + 2 не равно 15. Значит, тоже не подходит. 3) Если 12 рублей, то тогда карандаш стоит 12 : 4 = 3 рубля, а альбом 12 рублей. 12 + 3 =15.
По условию характеристические многочлены матриц второго порядка А и В совпадают. Поскольку характеристический многочлен ищется по формуле
Если бы корни характеристического уравнения были бы разные, все матрицы с таким характеристическим уравнением были бы подобны, то есть были бы матрицами одного и того же оператора. Но по условию это не так. Вывод: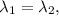
а матрицы второго порядка с таким условием бывают двух видов: - скалярная матрица (а поскольку по условию след равен 10, это скалярная матрица 5E, где E - единичная матрица), и те, которые подобны жордановой клетке с пятерками на диагонали. Поскольку определитель матрицы (как и ее след) не зависят от выбора базиса, делаем вывод, что определители матриц А и В равны 25.
ответ: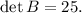
Замечание. Зачем было путать потенциальных "решателей" и писать в условии AA и BB вместо А и В? Не понимаю.
Замечание. Tr A - это обозначение для следа матрицы, то есть суммы элементов, стоящих на главной диагонали, det A - обозначение для определителя матрицы.
число рублей у Оли должно делиться без остатка на 4 и быть меньше 15.
Поэтому у нее може быть 4 рубля, или 8 рублей, или 12 рублей.
Подбираем: 1) если 4 рубля, то тогда карандаш стоит 4 :4 = 1 рубль, а альбом 4 рубля. 4 + 1 не равно 15. Значит, не подходит.
2) Если 8 рублей, то тогда карандаш стоит 8 : 4 = 2 рубля, а альбом 8 рублей.
8 + 2 не равно 15. Значит, тоже не подходит.
3) Если 12 рублей, то тогда карандаш стоит 12 : 4 = 3 рубля, а альбом 12 рублей.
12 + 3 =15.