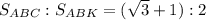Треугольник авс вписан в окружность.известно,что величина угла а равна 75 градусов, угла в равна 45 градусов.хорда ак составляет угол 15 градусов с хордой ас.найдите отношение площади треугольника авс к площади треугольника авк.
Рассмотрим случай, когда хорда АК лежит вне ∆АВС. Чертеж во вложении.
1) По теореме о сумме углов треугольника в ∆АВС ∠С=180°-45°-75°=60°.
2)∠ВКА=∠ВСА = 60° (опираются на одну и ту же дугу АВ). Поэтому в ∆АВК и ∆АВС ∠ВКА=∠ВСА, следовательно, площади тих треугольников пропорциональны произведениям сторон, образующих равные углы этих треугольников, т.е.
3) В ∆АВК ∠ВАК = 75°+15°=90°. Следовательно, ∆АВК - прямоугольный, а гипотенуза ВК является диаметром окружности.
В ∆АВК ∠АВК = 90°-60°=30°, значит, гипотенуза ВК=2АК.
4) В ∆АВС по теореме синусов
5) ∆ВCК-прямоугольный, ∠ВСК = 90° (опирается на полуокружность, либо по свойству противоположных углов вписанного четырехугольника).
∠КВС=∠АКС = 15° (опираются на одну и ту же дугу КС).
Рассмотрим случай, когда хорда АК лежит вне ∆АВС. Чертеж во вложении.
1) По теореме о сумме углов треугольника в ∆АВС ∠С=180°-45°-75°=60°.
2)∠ВКА=∠ВСА = 60° (опираются на одну и ту же дугу АВ). Поэтому в ∆АВК и ∆АВС ∠ВКА=∠ВСА, следовательно, площади тих треугольников пропорциональны произведениям сторон, образующих равные углы этих треугольников, т.е.
3) В ∆АВК ∠ВАК = 75°+15°=90°. Следовательно, ∆АВК - прямоугольный, а гипотенуза ВК является диаметром окружности.
В ∆АВК ∠АВК = 90°-60°=30°, значит, гипотенуза ВК=2АК.
4) В ∆АВС по теореме синусов
5) ∆ВCК-прямоугольный, ∠ВСК = 90° (опирается на полуокружность, либо по свойству противоположных углов вписанного четырехугольника).
∠КВС=∠АКС = 15° (опираются на одну и ту же дугу КС).
Поэтому ВС=BK*cos15°
6) Итак,
ответ: