Три тракториста вспахали поле площадью 940 га. Сколько га вспахал первый тракторист , если он вспахал 35% всего поля

Показать ответ

Ответ:

Gorodnichevavi

07.12.2020 01:45

а) 4x+y=8

3x+2y=11

Согласно первому уравнению у = 8 - 4x, подставим это значение y во второе уравнение:

3x+2(8 - 4x)=11

3x + 16 - 8x = 11

5x = 5

x = 1

Значит y = у = 8 - 4 · 1 = 4

ответ: (1; 4)

б) 8x+3y=-7

-4x-y=5

Cкладываем два уравнения:

8x + (-4x) + 3y + (-y) = -7 + 5

4x + 2y = -2

2(2x + y) = -2

2x + y = -1

y = -1 - 2x

Полностью решить уравнение методом сложения не удалось, так что прибегаем к методу подставновки и подставляем полученное значение y в ондо из уравнений. Допустим, во второе:

-4x-(-1 - 2x)=5

-2x = 4

x = -2

Значит y = -1 - 2(-2) = 3

ответ: (-2; 3)

0,0(0 оценок)

Ответ:

Turtygin

12.06.2021 10:08

$\left \{ {{x+y=8} \atop {2x+5y=22}} \right.$ ⇔ Умножим первую часть на -1 ⇔ $+\left \{ {{-x-y=-8} \atop {2x+5y=22}} \right.$ ⇔ Получим новое уравнение, которое пойдёт первым в новой системе ⇔ x+4y=14

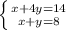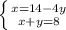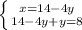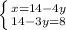Cоставим новую систему неравенств. Для облегчения нахождения неизвестного возьмём первое в данном: $\left \{ {{x+4y=14} \atop {x+y=8}} \right.$ ⇔ Выразим х из первого уравнения: $\left \{ {{x=14-4y} \atop {x+y=8}} \right.$ ⇔ Подставим х из первого уравнения во второе ⇔ $\left \{ {{x=14-4y} \atop {14-4y+y=8}} \right.$ ⇔ Упростим второе уравнение: $\left \{ {{x=14-4y} \atop {14-3y=8}} \right.$ ⇔ Перенесём числа во втором уравнении в правую часть: $\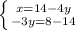left \{ {{x=14-4y} \atop {-3y=8-14}} \right.$ ⇔ $\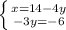left \{ {{x=14-4y} \atop {-3y=-6}} \right.$ ⇔ $\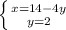left \{ {{x=14-4y} \atop {y=2}} \right.$ Нашли первое неизвестное, теперь подставим его в первое уравнение системы: $\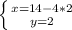left \{ {{x=14-4*2} \atop {y=2}} \right.$ ⇔ Теперь легко найдём второе неизвестное системы: $\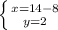left \{ {{x=14-8} \atop {y=2}} \right.$ ⇔ $\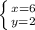left \{ {{x=6} \atop {y=2}} \right.$

Проверка:

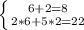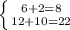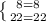Если х=6, а y=2, то $\left \{ {{6+2=8} \atop {2*6+5*2=22}} \right.$ ⇔ $\left \{ {{6+2=8} \atop {12+10=22}} \right.$ ⇔ $\left \{ {{8=8} \atop {22=22}} \right.$ ⇒ Система уравнений решена верно.