Пошаговое объяснение:
здесь нам потребуется определение операций над множествами и понятие пустого множества
объединение множеств А∪В - это множество, содержащее в себе все элементы исходных множеств А и В
разность множеств А\В - это множество, содержащее все элементы множества А, не входящие в множество В
пустое множество -это множество не содержащее ни одного элемента
объединение любого исходного множества с пустым множеством - это множество, содержащее элементы исходного множества
пересечение множеств А∩В – это множество, которое состоит из всех общих элементов исходных множеств А и В
1) А = {a,b,c} B = {v,d,s} A∪B = {a,b,c,v,d,s}
ответ B)
2)
ответ А)
3) A = {1,5,6} B = {7,5,2} C = {6,8,2}
(A\B)∩C
(A\B) = {1,6}
(A\B)∩C = {6}
ответ Б)
Пошаговое объяснение:
здесь нам потребуется определение операций над множествами и понятие пустого множества
объединение множеств А∪В - это множество, содержащее в себе все элементы исходных множеств А и В
разность множеств А\В - это множество, содержащее все элементы множества А, не входящие в множество В
пустое множество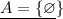
-это множество не содержащее ни одного элемента
объединение любого исходного множества с пустым множеством - это множество, содержащее элементы исходного множества
пересечение множеств А∩В – это множество, которое состоит из всех общих элементов исходных множеств А и В
1) А = {a,b,c} B = {v,d,s} A∪B = {a,b,c,v,d,s}
ответ B)
2)
ответ А)
3) A = {1,5,6} B = {7,5,2} C = {6,8,2}
(A\B)∩C
(A\B) = {1,6}
(A\B)∩C = {6}
ответ Б)