Здесь нужно просто перевести нетипичные данные в нормальные, привычные единицы измерения. Разность скоростей велосипеда и мотоцикла - 500 метров в минуту. Если умножить на 60, то получим, что разность скоростей равна 30 км/ч, что более привычно и понятно. Примем скорость велосипеда за х. Тогда скорость мотоцикла равна х+30 Время перемещения на 120 км: 120/х = 120/(х+30) +2 Умножим на х (х+30) 120 (х+30) = 120х + 2х^2 + 60х Получилось квадратное уравнение 2х^2 + 60х - 3600 = 0 У уравнения два решения, но смысл имеет только одно из них, положительное, х=30 ответ: скорость велосипедиста равна 30 км/ч
Разность скоростей велосипеда и мотоцикла - 500 метров в минуту. Если умножить на 60, то получим, что разность скоростей равна 30 км/ч, что более привычно и понятно.
Примем скорость велосипеда за х.
Тогда скорость мотоцикла равна х+30
Время перемещения на 120 км:
120/х = 120/(х+30) +2
Умножим на х (х+30)
120 (х+30) = 120х + 2х^2 + 60х
Получилось квадратное уравнение
2х^2 + 60х - 3600 = 0
У уравнения два решения, но смысл имеет только одно из них, положительное, х=30
ответ: скорость велосипедиста равна 30 км/ч
Відповідь:
Покрокове пояснення:
а1 - проекція катета а на гіпотенузу
b1 - проекція катета b на гіпотенузу
a^2 = c*a1; b^2 c*b
а) c = 6 + 24 = 30 см
a^2 = 30*6 = 180
a =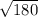 = 6
= 6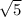 см
см
b^2 = 30*24 = 720
b =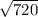 = 12
= 12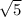 см
см
б) c = 12 + 16 = 28
a^2 = 28*12 = 336
a =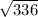 = 16
= 16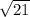 см
см
b^2 = 28*16 = 448
b =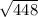 = 16
= 16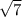 см
см
в) c = 8 + 10 = 18 см
a^2 = 18*8 = 144
a =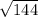 = 12 см
= 12 см
b^2 = 18*10 = 180
b =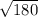 = 6
= 6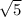 см
см
г) c = 3 + 23 = 26
a^2 = 26*3 = 78
a =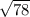 см
см
b^2 = 26*23 = 598
b =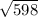 см
см