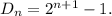У Каті були гроші. У перший день вона витратила 4/10 усіх грошів . У другий день — 3/12 від решти коштів. В третій день витратила те, що залишилося , а саме 90 грн. Скільки грошей всього було у Каті спочатку?
Обозначим этот определитель через Раскладывая его по первой строке, получаем
(последнее равенство получено с разложения по первому столбцу). Конечно, в этом равенстве предполагается, что n>2.
Непосредственно ищем используя выведенную формулу, находим Замечаем такую закономерность:
Естественно возникает гипотеза, что для любого натурального n
Докажем это. Для начальных значений n гипотеза уже проверена, остается проверить индукционный переход. А именно, предположив, что гипотеза верна при n=k и n=k+1, докажем, что тогда она верна и при n=k+2. В самом деле,
Тем самым гипотеза доказана при всех натуральных n.
Замечание. Задачу можно было бы решить с характеристического уравнения, но в этом случае пришлось бы слишком много объяснять.
18 минут
Пошаговое объяснение:
Коля 45 мин.
папа 36 мин.
повышение пр-ти 1/9
время вместе?
Решение
1 работа по вскопке одной грядки
1 : 45 = 1/45 (гр./мин.) производительность Коли
1 : 36 = 1/36 (гр./мин.) производительность папы
1/45 + 1/36 = (4+5)/180 = 9/180 = 1/20 (гр./мин.) совместная производительность без учета повышения.
1/20 * 1/9 = 1/180 (гр./мин.) повышение производительности при совместной вскопке.
1/20 + 1/180 = (9+1)/180 = 10/180 = 1/18 (гр./мин.) реальная производительность
1 : (1/18) = 1 * (18/1) = 18 (мин.) реальное время вскопки грядки
ответ: 18 мин.
Обозначим этот определитель через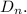 Раскладывая его по первой строке, получаем
Раскладывая его по первой строке, получаем
(последнее равенство получено с разложения по первому столбцу). Конечно, в этом равенстве предполагается, что n>2.
Непосредственно ищем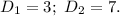 используя выведенную формулу, находим
используя выведенную формулу, находим 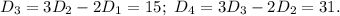 Замечаем такую закономерность:
Замечаем такую закономерность:
Естественно возникает гипотеза, что для любого натурального n
Докажем это. Для начальных значений n гипотеза уже проверена, остается проверить индукционный переход. А именно, предположив, что гипотеза верна при n=k и n=k+1, докажем, что тогда она верна и при n=k+2. В самом деле,
Тем самым гипотеза доказана при всех натуральных n.
Замечание. Задачу можно было бы решить с характеристического уравнения, но в этом случае пришлось бы слишком много объяснять.
ответ: