Первая бригада может покрасить забор за 18 дней, а вторая за 24 дня. Первая бригада работала над выполнением этого задания 6 дней, после чего вторая бригада закончила работу. За сколько всего дней было выполнено задание?
Решение
1) Рассчитаем, какую часть задания выполнила первая бригада:
6 : 18 = 1/3.
2) Следовательно, второй бригады надо было выполнить оставшуюся часть задания, что составляет:
1 - 1/3 = 2/3 всей работы.
3) Второй бригаде для выполнения всей работы потребовалось бы 24 дня. Рассчитаем, сколько дней необходимо второй бригаде для того, чтобы выполнить оставшиеся 2/3 задания:
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда
По условию BE - биссектриса и по свойству биссектрисы
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
Теперь можем найти
(ед.).
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
22 дня
Пошаговое объяснение:
Задание
Первая бригада может покрасить забор за 18 дней, а вторая за 24 дня. Первая бригада работала над выполнением этого задания 6 дней, после чего вторая бригада закончила работу. За сколько всего дней было выполнено задание?
Решение
1) Рассчитаем, какую часть задания выполнила первая бригада:
6 : 18 = 1/3.
2) Следовательно, второй бригады надо было выполнить оставшуюся часть задания, что составляет:
1 - 1/3 = 2/3 всей работы.
3) Второй бригаде для выполнения всей работы потребовалось бы 24 дня. Рассчитаем, сколько дней необходимо второй бригаде для того, чтобы выполнить оставшиеся 2/3 задания:
24 · (2/3) = 48 : 3 = 16 дней.
4) Всю работу выполняли:
первая бригада - в течение 6 дней,
вторая бригада - в течение 16 дней.
Следовательно, всё задание было выполнено за:
6 + 16 = 22 дня.
ответ: всё задание было выполнено за 22 дня
Пошаговое объяснение:
Дано (см. рисунок):
ΔABC
BE - биссектриса
AD - медиана
BE⊥AD
BE=AD=16 (ед.)
Найти AB, BC, CA.
Решение.
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда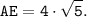
По условию BE - биссектриса и по свойству биссектрисы
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
Теперь можем найти
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
AB²=AO²+OB²=8²+12²=64+144=208=4²·13,
откуда
Из AB=BC/2 находим: