У треугольника все стороны равны друг другу. На одной из сторон треугольника построен прямоугольник, площадь которого равна 192 см кв, а одна из его сторон 24 см. Сторона прямоугольника совпадает со стороной треугольника. Найдите площадь квадрата, периметр которого равен периметру получившейся фигуры. Запишите развернутый ответ по действиям (укажите

Показать ответ

Ответ:

катя4003

17.07.2022 00:44

x∈(-4/3; 1/3)

Пошаговое объяснение:

Это квадратное неравенство. Для начала ищем дискриминант по формуле D=b^2-4ac

D=2^2-4*3*(-1)=4+12=16=4^2

Ищем x по формуле x1,2=(-b+\sqrt{D} )/2a

x1=(-2 + 4)/6=1/3

x2=(-2 - 4)/6=-4/3

Выставляем это на числовой прямой

+ -4/3 - 1/3 +

Расставляем знаки путём подстановки чисел из этих промежутков в начальное уравнение (к примеру -10,0,10).

Поскольку у нас знак \leq, то ищем отрицательный участок (со знаком минус). Это от -4/3 до 1/3.

x∈(-4/3; 1/3)

0,0(0 оценок)

Ответ:

Лешик2005

01.03.2021 09:26

Решение 1

Преобразуем сумму в произведение по формуле

$\cos x+\cos y=2\cos\dfrac{x-y}2\cos\dfrac{x+y}2$

Попробуем получить что-нибудь похожее в правой части первого уравнения. Пригодятся формулы преобразования суммы косинусов в произведение и формула для косинуса двойного угла:

$\sin x\sin y=\dfrac12\left(\cos(x-y)-\cos(x+y)\right)=\dfrac12\left(\left(2\cos^2\dfrac{x-y}2-1\right)-\right.\\\left.-\left(2\cos^2\dfrac{x+y}2-1\right)\right)=\cos^2\dfrac{x-y}2-\cos^2\dfrac{x+y}2$

Таким образом, если обозначить косинус полусуммы за s, а косинус полуразности за a, получится система

$\begin{cases}2as=1\\a^2-s^2=\dfrac34\end{cases}$

Из первого уравнения системы a = 1/(2s), подставляем во второе уравнение и после преобразований получаем биквадратное уравнение:

$1-4s^4=3s^2\\4(s^2)^2+3s^2-1=0$

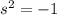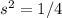По теореме Виета угадываем, что s^2=-1 или s^2=1/4 ; первый вариант не даёт вещественных решений, из второго следует 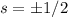$s=\pm1/2$ , тогда $a=\pm1$ . Возвращаемся обратно к x и y:

1) s = 1/2, a = 1:

$\begin{cases}\cos\dfrac{x+y}2=\dfrac 12\\\cos\dfrac{x-y}2=1\end{cases}\Leftrightarrow\begin{cases}x+y=\pm\dfrac{2\pi}3+4\pi n', n'\in\mathbb Z\\x-y=4\pi n'', n''\in\mathbb Z\end{cases}\Leftrightarrow\\\Leftrightarrow\begin{cases}x=\pm\dfrac{\pi}3+2\pi (n'+n'')\\y=\pm\dfrac{\pi}3+2\pi (n'-n'')\end{cases}, n', n''\in\mathbb Z$

2) s = -1/2, a = -1:

$\begin{cases}\cos\dfrac{x+y}2=-\dfrac 12\\\cos\dfrac{x-y}2=-1\end{cases}\Leftrightarrow\begin{cases}x+y=2\pi\pm\dfrac{2\pi}3+4\pi m', m'\in\mathbb Z\\x-y=2\pi+4\pi m'', m''\in\mathbb Z\end{cases}\Leftrightarrow\\\Leftrightarrow\begin{cases}x=2\pi\pm\dfrac{\pi}3+2\pi (m'+m'')\\y=\pm\dfrac{\pi}3+2\pi (m'-m'')\end{cases}, m', m''\in\mathbb Z$

Можно переписать все полученные решения в виде

$\left(\pm\dfrac\pi3+2\pi n,\pm\dfrac\pi3+2\pi m\right)$ , где $n,m\in\mathbb Z$ .

Решение 2

Возведём второе уравнение в квадрат, применим основное тригонометрическое тождество:

$(1-\cos^2x)(1-\cos^2y)=\dfrac9{16}\\(1-\cos x)(1+\cos x)(1-\cos y)(1+\cos y)=\dfrac9{16}$

Из первого уравнения сумма косинусов 1, так что 1 - один косинус = другой косинус.

$\cos x\cos y (1+\cos x)(1+\cos y)=\dfrac{9}{16}\\\cos x\cos y(1+\cos x+\cos y+\cos x\cos y)=\dfrac9{16}\\\cos x\cos y(2+\cos x\cos y)=\dfrac9{16}$

Получилось квадратное уравнение на cos x cos y, его корни -9/4 и 1/4. Произведение косинусов по модулю не больше 1, так что единственный вариант cos x cos y = 1/4. Совместно с cos x + cos y = 1 получаем, что соs x = cos y = 1/2, откуда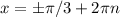 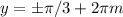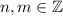$x=\pm\pi/3+2\pi n$ , $y=\pm \pi/3+2\pi m$ , $n,m\in \mathbb Z$ , знаки + и - выбираются независимо.

В этом решении был неравносильный переход при возведении в квадрат, могли появиться посторонние решения. Подставляя в исходную систему, получаем, что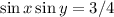 $\sin x\sin y=3/4$ , только если в обоих значениях выбрать одинаковые знаки.