Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1)
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
2)
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3)
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.
Вычислим ширину прямоугольника
b=40*5/8=40*5:8=200:8=25 (м)-ширина
Длина забора,это периметр прямоугольника.Периметр находится по формуле
Рпр=(а+b)*2,где a-длина, b-ширина
Рпр=(40+25)*2=65*2=130 (м)
ответ:130 м длина забора вокруг площадки
№2
Вычислим разницу работы насосов
18-12=6(мин)
Значит насос за 6 мин накачал 30 ведер воды
Вычислим сколько воды накачал 1 насос за 12 мин (6мин*2)
30*2=60 (в)
Вычислим сколько воды накачал 2 насос за 18 мин(6мин*3)
30*3=90 (в)
ответ:60 ведер воды накачал 1 насос;90 ведер воды накачал 2 насос
Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1)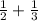
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
2)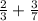
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3)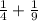
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
2)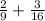
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.