У1) каждое из следующих чисел является одним из корней квадратного
уравнения с целыми коэффициентами. найдите другой корень. запи-
шите решение с объяснением.
а) –2 + v3 b) 25 +1 с) 3 – 7 d) m + уп
2) составьте квадратное уравнение с целыми коэффици-
ентами, один из корней которого является число 2 – 3

Показать ответ

Ответ:

Маріямарія

24.08.2020 05:01

Пошаговое объяснение:

1дм = 10см, 1дм³=10*10*10см³=1000см³

45дм³-59см³=45000см³-59см³=

=44941см³=44дм³ 941см³

1м=10дм, 1м³=10*10*10дм³=1000дм³

74м³-145дм³=74000дм³-145дм³=

=73855дм³=73м³ 855дм³

1см=10мм, 1см³=10*10*10мм³=1000мм³

50см³-35мм³=50000мм³-35мм³=

=49965мм³=49см³ 965мм³

1см³=1000мм³(смотри пункт 3)

10см³-63мм³=10000мм³-63мм³=

=9937мм³=9см³937мм³

1м=10дм, 1дм=10см,

1м=10*10см=100см

1м³=100*100*100см³=1000000см³

1м³-4750см³=1000000см³-4750см³=

=995250см³=995дм³250см

1см³=1000мм³(смотри пункт 3)

63см³-609мм³=63000мм³-609мм³=

=62391мм³=62см³391мм³

0,0(0 оценок)

Ответ:

798210374

19.02.2020 11:28

$F_0=0,F_1=1, F_n=F_{n-1}+F_{n-2}, n\in N\backslash\{1\}$

Заметим, что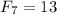 F_7=13

Докажем, что, начиная с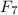 F_7 , последовательность Фибоначчи периодическая по модулю 1000.

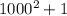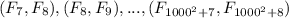Рассмотрим 1000^2+1 пару чисел $(F_7,F_8),(F_8,F_9),...,(F_{1000^2+7},F_{1000^2+8})$ .

Каждое из чисел каждой из пар дает один из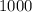 1000 остатков по модулю 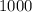1000 . Тогда всего вариантов пар остатков от деления на 1000 может быть 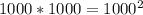1000*1000=1000^2 (1000 вариантов остатков 1ого числа пары и 1000 вариантов у 2ого).

Тогда, по принципу Дирихле, в рассматриваемом мн-ве пар найдутся хотя бы 2 пары чисел, соответствующие элементы которых сравнимы по модулю 1000 - а, с учетом определения последовательности Фибоначчи, это и означает периодичность остатков ее членов по модулю 1000.

Возьмем 2 такие пары с наименьшими номерами. Пусть это пары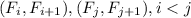 $(F_i,F_{i+1}), (F_j,F_{j+1}), i$ . Покажем, что i=7 .

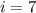Пусть не так, и .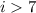

По построению,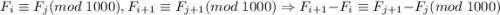 $F_i\equiv F_j(mod \;1000),F_{i+1}\equiv F_{j+1}(mod \;1000)\Rightarrow F_{i+1}-F_{i}\equiv F_{j+1}-F_{j}(mod \;1000)$

Но, по определению последовательности Фибоначчи,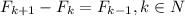 $F_{k+1}-F_{k}=F_{k-1},k\in N$ . А значит 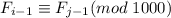$F_{i-1}\equiv F_{j-1}(mod\; 1000)$ . А тогда соответствующие элементы пар чисел 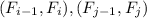$(F_{i-1},F_i),(F_{j-1},F_j)$ сравнимы по модулю 1000 - противоречие с тем, что 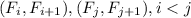$(F_i,F_{i+1}), (F_j,F_{j+1}), i$ - пары с наименьшими номерами.

Значит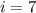 i=7 .

А это означает, что в последовательности остатков от деления членов последовательности Фибоначчи на 1000 найдется сколь угодно чисел, сравнимых с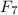 F_7 по модулю 1000. Т.к последовательность возрастающая и неограниченная, начиная со 2ого члена, это утверждение эквивалентно условию задачи.

Доказано.

________________________________

Можно доказать аналогичным образом и более общее утверждение: последовательность чисел Фибоначчи по модулю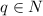 $q\in N$ периодическая (вышеприведенные рассуждения - частный случай этого док-ва). Длина периода такой последовательности обозначается 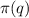$\pi(q)$ и называется период Пизано.