Ученик Юхан в компьютерной программе Geogebra построил равнобедренный треугольник АВС. Длина боковой стороны ВС треугольника равна 10 см, а угол при вершине АСВ равен 640 . К боковой стороне ВС Юхан провёл высоту, которая разделила Треугольник АВС на две части: треугольники АВD и АСD. Юхан предположил, что площадь треугольника АВD в 2 раза больше площади треугольника АСD. Вычислить площади треугольников АВD и АСD и выяснить. Прав ли был Юхан?
Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
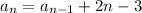, где n - число лучей кратное 3.
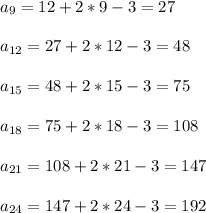
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле:
Пробуем вычислить по этой формуле:
Итак, для 24 лучей возможно максимум 192 тупых угла.
Система не имеет решения, если графики уравнений системы не имеют общих точек ( не пересекаются и не касаются)
Для двух линейных уравнений
1) ах+ву =с
2) mx+ny =k
Система не имеет решений, если коэффициенты при неизвестных пропорциональны, но не пропорциональны свободным членам: a /m = b/n ≠ c/к
П р и м е р . В системе уравнений
1)2х -3у =7
2)6х -9у = 12
Коэффициенты пропорциональны 2/6 = (-3)/ (-9) = 1/3
но отношение свободных членов 7 / 12 не равно 1 / 3.
Эта система не имеет решений
Пошаговое объяснение: