Ученику необходимо определить объем жидкости. Для этого он пользуется мензуркой, которая изображена на рисунке. A) Определите цену деления шкалы мензурки.
Цена деления [1]
B) Запишите объем жидкости с учетом погрешности.
V = [2]
Ученику необходимо определить объем жидкости. Для этого он пользуется мензуркой, которая изображена на рисунке.
Количество конфет кратно 5, но не кратно 2, 3 и 4. Числа 10, 15, 20, 30 и 40 не подходят - они делятся без остатка на одно из чисел 2, 3 или 4. Варианты: 5 конфет, 25 конфет, 35 конфет. Если конфет 5, то при вычитании 3 получится остаток 2, что противоречит условиям. Так же не получится подобным образом разложить 35 конфет: если раскладывать по 3, получится остаток 2 (3*11 = 33), если по 4 - остаток 3 (4*8 = 32). Остаётся только вариант 25, который нам вполне подходит: 25:2 = 12 ост 1 25:3 = 8 ост 1 25:4 = 6 ост 1.
ответ: Увеличение на: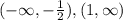
Убывает на: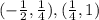 .
.
Пошаговое объяснение: Найдем производную.
Приравняем производную к 0.
Решим относительно x.
Упростим числитель.
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
и упростим.
Решим уравнение.
Разлагаем на множители левую часть уравнения.
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
Приравняем x-1 к 0, затем решим относительно x.
Приравняем 2x+1 к 0, затем решим относительно x.
Решение является результатом x-1=0 и 2x+1=0.
Значения, которые обращают производную в 0 - 1,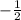 .
.
1,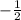 .
.
Выясним, при каких значениях переменной функция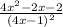 не определена.
не определена.
Разобьем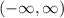 на интервалы вокруг значений x, в которых производная равна 0 или не определена.
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
Подставим значение из интервала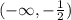 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на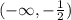 , так как
, так как 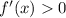 .
.
Подставим значение из интервала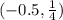 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Убывает на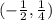 , поскольку
, поскольку 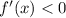
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на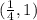 , поскольку
, поскольку 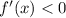
Подставим значения из интервала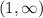 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на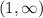 , так как
, так как 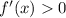 .
.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: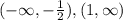
Убывает на: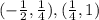
Варианты: 5 конфет, 25 конфет, 35 конфет.
Если конфет 5, то при вычитании 3 получится остаток 2, что противоречит условиям.
Так же не получится подобным образом разложить 35 конфет: если раскладывать по 3, получится остаток 2 (3*11 = 33), если по 4 - остаток 3 (4*8 = 32).
Остаётся только вариант 25, который нам вполне подходит:
25:2 = 12 ост 1
25:3 = 8 ост 1
25:4 = 6 ост 1.
ответ: 25 конфет.