Математика: Укажіть похідну y = x(x³ +1)

Укажіть похідну y = x(x³ +1)

Показать ответ

Ответ:

NastyaKovalenkoo

08.09.2022 23:13

Старпом - : старший капитана во 2 знач.)
Хотя, если надо. Выдаю все результаты, выбери любой понравившийся.
старпом
гарсон
матрос
монстр
морган
намост
нарост
пастор
патрон
пробст
романс
ротанг
собрат
стогна
строма
стропа
тампон
тонарм
торбан
торбас
оп-арт
аборт
ангоб
апорт
аргон
артос
багор
барон
басон
бастр
батог
батон
борат
гамон
гнома
горст
грант
магот
манго
манор
манто
марго
масон
могар
набор
напор
норма
обман
обрат
онагр
орган
орнат
осман
остан
пагон
паром
пасмо
проба
роман
ротан
сабор
самбо
сапог
сарон
сбора
смотр
согра
спора
спорт
стопа
строп
табор
танго
томан
топар
торба
трамп
транс
тромб
тромп
тропа
агор
апсо
арго
атом
бант
барм
барн
барс
бона
бора
борт
брас
брат
бром
гарт
гном
гонт
гора
горб
горн
гост
граб
гран
грат
гроб
гром
грот
маго
мант
марс
март
мопс
морг
морс
мост
наос
наст
натр
нога
нома
нора
нота
омар
оспа
парс
пасо
пора
порт
пост
рамс
ранг
рант
рапс
роба
рога
ромб
роса
рост
рота
сабо
саго
сбор
сгон
смог
сноб
сноп
сома
сона
сонг
сонм
сопа
сорт
спор
спот
срам
стан
стог
стон
стоп
тога
тора
торг
торн
торс
трап
трас
трог
трон
троп
трос
амт
ант
бар
бас
бат
боа
бог
бон
бор
бот
бра
гам
гап
гон
гот
маг
мар
мат
мга
моа
мор
мот
нар
ном
нос
опт
орс
орт
оса
ост
пан
пар
пас
пат
пом
пот
раб
рог
ром
роп
рот
сан
сап
сом
сон
сор
сот
тар
том
тон
топ
тор
ар
ас
ат
го
ма
мо
ом
ор
па
ро
та

0,0(0 оценок)

Ответ:

Ариана16112001

08.09.2022 23:13

Предположим, что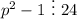 $p^2-1~\vdots ~24$ . Тогда и 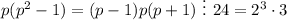$p(p^2-1)=(p-1)p(p+1)~\vdots ~24=2^3\cdot 3$ . Проверим последнее утверждение.

Данное произведение — это произведение трёх последовательных чисел, значит, один из множителей обязательно делится на 3. Так как p простое и больше 3, p-1 и p+1 чётны. Докажем, что произведение p-1 = 2k и p+1 = 2k+2 (k ∈ N) делится на 8:

2k(2k+2)=4k(k+1) . Оно, очевидно, делится на 4. Также оно делится ещё на 2, так как одно из чисел k и k+1 обязательно чётное.

$p(p^2-1)~\vdots~3,~p^2-1~\vdots~8\Rightarrow p(p^2-1)~\vdots~24$ .

Однако из этого не обязательно следует, что и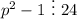 $p^2-1~\vdots~24$ . Но p > 3 и p — простое, значит, p не содержит множителей числа 24, то есть на 24 может делиться только 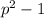p^2-1 , что и требовалось доказать.