. Рассмотрим прямоугольный треугольник со сторонами
(последняя - гипотенуза). Из него видно, что , а . Тогда исходный синус перепишется в виде .
Рассмотрим треугольник с гипотенузой и катетом . Тогда оставшийся катет можно вычислить по теореме Пифагора: . Пусть рационально и . Тогда у треугольника рациональные стороны и синус одного из его углов удовлетворяет требованиям. Теперь достаточно увеличить его стороны в наименьшее общее кратное всех трех знаменателей раз. И требуемый треугольник готов
Для решения этой задачи нужно найти число, которое одновременно делилось на 80, 90 и 120, т.е. нужно посчитать наименьшее общее кратное НОК(80, 90, 120). Только при этом условии маршрутки встретятся, т.к. им нужно затратить одинаковое время до встречи.
Рассмотрим треугольник с гипотенузой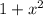 и катетом
и катетом 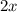 . Тогда оставшийся катет можно вычислить по теореме Пифагора:
. Тогда оставшийся катет можно вычислить по теореме Пифагора: 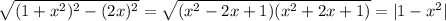 . Пусть
. Пусть  рационально и
рационально и 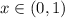 . Тогда у треугольника рациональные стороны и синус одного из его углов удовлетворяет требованиям. Теперь достаточно увеличить его стороны в наименьшее общее кратное всех трех знаменателей раз. И требуемый треугольник готов
. Тогда у треугольника рациональные стороны и синус одного из его углов удовлетворяет требованиям. Теперь достаточно увеличить его стороны в наименьшее общее кратное всех трех знаменателей раз. И требуемый треугольник готов
Г) 20.00
Пошаговое объяснение:
Для решения этой задачи нужно найти число, которое одновременно делилось на 80, 90 и 120, т.е. нужно посчитать наименьшее общее кратное НОК(80, 90, 120). Только при этом условии маршрутки встретятся, т.к. им нужно затратить одинаковое время до встречи.
Разложим на множители числа
120 = 5 * 3 * 2 * 2 * 2
90 = 5 * 3 * 3 * 2
80 = 5 * 2 * 2 * 2 * 2
НОК(80, 90, 120) = 5 * 3 * 2 * 2 * 2 * 3 * 2 = 720
720 мин = 720 : 60 = 12 часов - через это время они встретятся
8 + 12 = в 20 часов маршрутки снова встретятся