Здравствуйте!
110
Пошаговое объяснение:
Вспомним определение факториала:
Значит значение (n-2)! равно:
Произведение есть и в числителе, и в знаменателе, поэтому сокращаем его.
У нас останется:
Подставляем значение n=11:
факториал числа это число * факториал (числа -1)
n!/(n-2)!=n(n-1)!/(n-2)!=n(n-1)(n-2)!/(n-2)!=n(n-1)=11*(11-1)=11*10=110
Здравствуйте!
110
Пошаговое объяснение:
Вспомним определение факториала:
Значит значение (n-2)! равно:
Произведение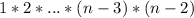
есть и в числителе, и в знаменателе, поэтому сокращаем его.
У нас останется: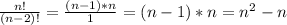
Подставляем значение n=11:
факториал числа это число * факториал (числа -1)
n!/(n-2)!=n(n-1)!/(n-2)!=n(n-1)(n-2)!/(n-2)!=n(n-1)=11*(11-1)=11*10=110