ответ:Чтобы решить это уравнение, разделите знаменатели на множители и с квадратичной формулы найдите два действительных корня, которые дадут значение x.
Пошаговое объяснение:
Чтобы решить это уравнение, нужно разложить знаменатели дробей. Уравнение имеет вид Затем мы можем умножить обе стороны уравнения на и разложить левую часть, в результате чего получим полиномиальное уравнение степени 1004. Чтобы решить это уравнение, нам нужно воспользоваться квадратичной формулой для нахождения корней многочлена. В результате мы получим два вещественных корня, которые и дадут значение x.
Квадратичная формула - это математическое уравнение, используемое для решения корней полиномиального уравнения степени два. Она гласит, что для любого квадратного уравнения. два корня можно найти по следующей формуле: x = (-b ± √(b^2 - 4ac)) / 2a, где a, b и c - коэффициенты полиномиального уравнения. Знак ± указывает на то, что уравнение может иметь два различных решения в зависимости от выбранного знака.
ответ:Чтобы решить это уравнение, разделите знаменатели на множители и с квадратичной формулы найдите два действительных корня, которые дадут значение x.
Пошаговое объяснение:
Чтобы решить это уравнение, нужно разложить знаменатели дробей. Уравнение имеет вид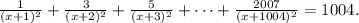 Затем мы можем умножить обе стороны уравнения на
Затем мы можем умножить обе стороны уравнения на  и разложить левую часть, в результате чего получим полиномиальное уравнение степени 1004. Чтобы решить это уравнение, нам нужно воспользоваться квадратичной формулой для нахождения корней многочлена. В результате мы получим два вещественных корня, которые и дадут значение x.
и разложить левую часть, в результате чего получим полиномиальное уравнение степени 1004. Чтобы решить это уравнение, нам нужно воспользоваться квадратичной формулой для нахождения корней многочлена. В результате мы получим два вещественных корня, которые и дадут значение x.
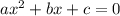 два корня можно найти по следующей формуле: x = (-b ± √(b^2 - 4ac)) / 2a, где a, b и c - коэффициенты полиномиального уравнения. Знак ± указывает на то, что уравнение может иметь два различных решения в зависимости от выбранного знака.
два корня можно найти по следующей формуле: x = (-b ± √(b^2 - 4ac)) / 2a, где a, b и c - коэффициенты полиномиального уравнения. Знак ± указывает на то, что уравнение может иметь два различных решения в зависимости от выбранного знака.
Квадратичная формула - это математическое уравнение, используемое для решения корней полиномиального уравнения степени два. Она гласит, что для любого квадратного уравнения.
_24759!3 _7948!4 _3190!5 _4152!6
24 !8253 4 !1987 30 !638 36 !692
_7 _ 39 _19 _55
6 36 15 54
_15 _34 _40 _12
15 32 40 12
_9 _28 0 0
9 28
0 0