ответ: Пусть скорость байдарки в стоячей воде = х км/ч. Тогда туристы плыли по течению со скоростью (х+3) км/ч, а против течения со скоростью (х-3) км/ч. Расстояние, которое туристы проплыли по течению = (2,4 х (умножить) (х+3)) км, а против течения (0,8 х (х-3)) км. Зная, что по течению туристы проплыли на 19,2 км больше, составим и решим уравнение.
ответ: Пусть скорость байдарки в стоячей воде = х км/ч. Тогда туристы плыли по течению со скоростью (х+3) км/ч, а против течения со скоростью (х-3) км/ч. Расстояние, которое туристы проплыли по течению = (2,4 х (умножить) (х+3)) км, а против течения (0,8 х (х-3)) км. Зная, что по течению туристы проплыли на 19,2 км больше, составим и решим уравнение.
2,4 х (х+3) - 0,8 х (х-3) = 19,2
2,4х +7,2 - 0,8 х +2,4 =19,2
1,6х +9,6 = 19,2
1,6х = 9,6
х = 6
Значит, скорость байдарки в стоячей воде 6 км/ч.
Пошаговое объяснение:
ответ: 200 км.
Пошаговое объяснение:
Весь путь разделён на 3 части: 8/20, 7/20 и 50 км. То есть, кроме 50 км, у нас есть ещё
Весь путь равен 20/20 (=1; мы поделили его на 20 частей, взяли все эти части и получился весь путь). Тогда 50 км составляют
50 км =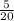
пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
10 км =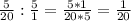
пути.
Одна двадцатая часть — 10 км. Семь двадцатых частей в семь раз больше, чем одна двадцатая часть:
Восемь двадцатых частей в восемь раз больше, чем одна двадцатая часть:
Обозначим весь путь за s. Тогда
s=I часть + II часть + III часть
s = 80 км + 70 км + 50 км = 200 км.
ответ: 200 км.