В арифметической прогрессии шестой член (который был равен 45) увеличили на 15. В результате получилось, что четвертый, пятый и шестой члены получившейся последовательности образовали геометрическую прогрессию. Найти сумму этих трех членов новой последовательности с четвертого по шестой. В случае не единственности решения выбрать наименьшую из возможных сумм. Полученное значение записать в бланк ответов в десятичной форме записи. ответ:
Характеристическое свойство арифметической прогрессии:
Характеристическое свойство геометрической прогрессии:
Рассмотрим арифметическую прогрессию с разностью d. Выпишем ее 4, 5 и 6 члены:
Выразим четвертый и пятый члены через шестой:
По условию известен шестой член:
Тогда имеем три последовательных члена арифметической прогрессии:
По условию, если шестой член увеличить на 15, то выписанные числа будут составлять уже геометрическую прогрессию.
Таким образом, три последовательных члена геометрической прогрессии:
Запишем для геометрической прогрессии характеристическое свойство:
Решаем уравнение:
Для первой ситуации с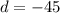 получим:
получим:
Для второй ситуации с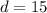 получим:
получим:
Наименьшая из возможных сумм равна 105.
ответ: 105