Имеется ввиду область допустимых значений. 1) x>/0 2x>/ -6 --> x>/-2 Нам подходит первое, т.к. только при выполнении второго в первом выражении допускается значения меньше 0. 2) 18-2х >/ 0 --> -2х>/ -18 --> х\< 9. 3) 10 - √(х-5) >/ 0 --> √(х-5)\<10 --> х - 5 \< 100 --> х \< 105 х - 5 >/ 0 --> х>/ 5 Т.е. хє[5;105] 7) x^2 + 3x + 1 >/0 D = 9-4 = 5 x1 = (-3+√5)/2 x2 = (-3-√5)/2 (x-(-3+√5)/2)(x-(-3-√5)/2) >/0 Методом интервалов хє(-беск; -3-√5)/2] U [(-3+√5)/2 ; + беск) 4) Методом интервалов: хє (-беск ; -3] U [8 ; +беск) 5) xєR 6) x>/ 3 x\< 1 x >/ -5/8 Пересечений нет, следовательно ни при каких. 8) для того, чтобы дробь была положительной нам нужно либо чтобы знаменатель и числитель были положительными, либо оба отрицательными. Получаем совокупность систем: x>/ -3 x< 4 либо x\< -3 x > 4 xє [-3;4) либо (-беск;-3] U (4; + беск)
1. НОД(А,В) = 2²⁸*3²⁹
НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸
2. а)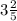 ; б)
; б) 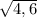
Пошаговое объяснение:
Задание 1.
А= 2³⁷*3¹⁵*12¹⁴ = 2³⁷*3¹⁵*(2²*3)¹⁴ = 2³⁷*3¹⁵*2²⁸*3¹⁴ = 2³⁷⁺²⁸ * 3¹⁵⁺¹⁴ = 2⁶⁵*3²⁹
В = 3⁷⁴ *10²⁸ = 3⁷⁴ *(2*5)²⁸ = 3⁷⁴*2²⁸*5²⁸
НОД(А,В) = 2²⁸*3²⁹
НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸
Задание 2.
a) x∈[√11; √13] и x∈Q (Q- множество рациональных чисел)
x=?
√11 ≈ 3,32 √13 ≈ 3,66
3,32 < x < 3,66
Например, x= 3,4 = 3 4/10 = 3 2/5 (∈Q)
x= 3,5 = 3 5/10 = 3 1/2 (∈Q)
x= 3,6 = 3 6/10 = 3 3/5 (∈Q)
(приведено сразу 3 примера такого рационального числа, на самом деле, их бесконечное множество).
б) x∈[2,1; 2,2], x∈I (I - множество иррациональных чисел)
2,1 = √(2,1)² = √4,41
2,2 = √(2,2)² = √4,84
√4,41 < x < √4,84
Например, х=√4,6 или х=√4,71 или х=√4,782 или х=√4,815
(приведено сразу 4 примера такого иррационального числа, на самом деле, их бесконечное множество).