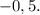В четырёхугольнике MNPK сторона = у см. 1.) выразите остальные стороны этого четырёхугольника , если:
а) NP на 5 см меньше MN,
б) PK в 3,25 раза больше MN,
в) MK на 5 см больше PK
2. Зная что периметр MNPK равен 25,5 и используя данные пункта 1, составьте уравнение.
3. решите уравнение полученное в пункте
2) Найдите длину MN

100 кораблей было в лилипутском флоте (Если цифры повторяются)

48 кораблей было в лилипутском флоте (Если цифры НЕ повторяются)

Пошаговое объяснение:

В задании не указано, повторяются цифры в 3-х значном числе или нет.

Если цифры повторяются:

Для первой цифры 3-х значного числа 4 варианта: 2; 4; 6; 8, т.к. с 0 число не начинается

Для второй и третьей цифры в числе по 5 вариантов: 0; 2; 4; 6; 8

Общее количество чисел: 4 * 5 * 5 = 100  

ответ: 100 кораблей было в лилипутском флоте

Если цифры не повторяются:

Для первой цифры 3-х значного числа 4 варианта: 2; 4; 6; 8, т.к. с 0 число не начинается.

Для второй цифры в числе подходят все 5 цифр, но т.к. одну из них уже использовали, остается 4 цифры.

Для третьей цифры остается только 3 варианта.

Общее количество чисел: 4 * 4 * 3 = 48

ответ: 48 кораблей было в лилипутском флоте

1. Уравнение вида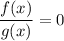 равносильно системе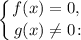

2. Решим уравнение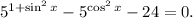

2.1. Поскольку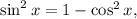 то

2.2. Используя свойство степеней имеем:

2.3. Сделаем замену: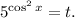 Тогда:

2.4. Преобразуем уравнение:

2.5. По теореме, обратной теореме Виета, имеем:

2.6. Делаем обратную замену:

2.7. Первое уравнение не имеет корней, поскольку правая часть не может быть отрицательной. Решим уравнение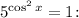

3. Определим ограничения: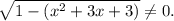

3.1. Ограничение для данного уравнения соответствует неравенству:

3.2. Раскроем скобки, приведем подобные слагаемые:

3.3. Умножим обе части неравенства на

3.4. Решением данного неравенства является промежуток

4. Отберем корни уравнения, принадлежащие промежутку

Пусть тогда

Пусть тогда

Пусть тогда

5. Решением данного уравнения является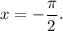

6. В ответ следует записать сумму корней (или корень, если он единственный), деленную на

ответ: