В данном множестве все элементы, кроме одного, обладают некоторым свойством. Опишите это свойство и найдите элемент, не обладающий им. а) {шар, цилиндр, круг, конус, сфера};
1. Подростковый возраст относится к так называемым критическим периодам жизни человека (периодам возрастного кризиса).Смысл подросткового кризиса заключается в том, что через борьбу за независимость от опеки взрослых человек удовлетворяет свои потребности в самопознании и самоутверждении. У него не просто возникает чувство уверенности в себе и полагаться на себя, но формируются поведения, позволяющие в дальнейшем справляться с жизненными трудностями.Психологи считают, что главным личностным изменением подросткового возраста является «чувство взрослости». Подросток желает быть взрослым и в то же время знает, что уровень его социальной готовности далеко не отвечает требованиям, предъявляемым к взрослому человеку. Отсюда и возникает противоречивость подросткового «чувства взрослости».В подростковом возрасте происходят процессы биологического созревания организма и социального взросления.
Обозначим скорость лодки как х, а скорость реки как y.
Нам известно, что путь S вычисляется по формуле S=v*t
Найдем сначала путь который шляпа за 15 минут
Sш=15*y Это путь который пройдет шляпа за 15 минут.
Найдем путь который пройдет лодка за 15 минут, т.к плывем против течения, то из скорости лодки вычитается скорость течения, значит скорость лодки против течения будет x-y. Теперь найдем путь:
Sл=15*(x-y)
Теперь найдем расстояние между шляпой и лодкой через 15 минут
Sобщ=15*(x-y)+15*y=15*x
Теперь рассматриваем момент, когда лодка плывет по течению. Ее скорость будет x+y (скорость лодки плюс скорость реки)
Так как шляпа плывет со скоростью реки и лодка плывет с собственной скоростью+скорость реки, то мы можем свести задачу к другой:
Найти время за которое лодка проплывет путь Sобщ при скорости x.
Это можно сделать потому что шляпа будет удаляться со скоростью у, а лодка будет к ней приближаться со скоростью х+у, значит можно считать что шляпа стоит, а лодка плывет к ней, но уже со скорость х.
Найдем теперь это время. Из формулы S=vt получаем, что t=S/v
Путь нам известен он равен Sобщ, скорость лодки нам тоже известна она равна х.(почему смотри выше)
Найдем время: минут
ответ: Лодка догонит шляпу через 15 минут, после того, как поплывет по течению
Обозначим скорость лодки как х, а скорость реки как y.
Нам известно, что путь S вычисляется по формуле S=v*t
Найдем сначала путь который шляпа за 15 минут
Sш=15*y Это путь который пройдет шляпа за 15 минут.
Найдем путь который пройдет лодка за 15 минут, т.к плывем против течения, то из скорости лодки вычитается скорость течения, значит скорость лодки против течения будет x-y. Теперь найдем путь:
Sл=15*(x-y)
Теперь найдем расстояние между шляпой и лодкой через 15 минут
Sобщ=15*(x-y)+15*y=15*x
Теперь рассматриваем момент, когда лодка плывет по течению. Ее скорость будет x+y (скорость лодки плюс скорость реки)
Так как шляпа плывет со скоростью реки и лодка плывет с собственной скоростью+скорость реки, то мы можем свести задачу к другой:
Найти время за которое лодка проплывет путь Sобщ при скорости x.
Это можно сделать потому что шляпа будет удаляться со скоростью у, а лодка будет к ней приближаться со скоростью х+у, значит можно считать что шляпа стоит, а лодка плывет к ней, но уже со скорость х.
Найдем теперь это время. Из формулы S=vt получаем, что t=S/v
Путь нам известен он равен Sобщ, скорость лодки нам тоже известна она равна х.(почему смотри выше)
Найдем время: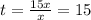 минут
минут
ответ: Лодка догонит шляпу через 15 минут, после того, как поплывет по течению