Вершины(пусть будут за "А" и "В") , которые имеют свои координаты в скобках , то - что находится левее ,принадлежит к оси Ох , то - что находится правее , принадлежит к оси Оу. Тогда А(-1 ; 0) ⇒ ( x = -1 ; y = 0 )Тогда А(-1 ; 0) ⇒ ( x = -1 ; y = 0 )B(4 ; 1) ⇒ (x = 4 ; y = 1 )
⠀⠀⠀⠀⠀(см. чертёж)
Вершины А и В противолежащии , чтобы найти площадь квадрата - нужно длину умножить на ширину , как видим , длина квадрата 1 (ед) , а ширина 4 (ед) , тогда S = 1 (eд) * 4 (ед) = 4 (ед²)
4 (ед²)
Пошаговое объяснение:
Вершины(пусть будут за "А" и "В") , которые имеют свои координаты в скобках , то - что находится левее ,принадлежит к оси Ох , то - что находится правее , принадлежит к оси Оу. Тогда А(-1 ; 0) ⇒ ( x = -1 ; y = 0 )Тогда А(-1 ; 0) ⇒ ( x = -1 ; y = 0 )B(4 ; 1) ⇒ (x = 4 ; y = 1 )⠀⠀⠀⠀⠀(см. чертёж)
Вершины А и В противолежащии , чтобы найти площадь квадрата - нужно длину умножить на ширину , как видим , длина квадрата 1 (ед) , а ширина 4 (ед) , тогда S = 1 (eд) * 4 (ед) = 4 (ед²)21 . Продлим d₂ влево .
∠НАС=110° , смежный с ним ∠САВ=180°-110°=70°
∠ВТЕ=95° , соответственный ему ∠АВС=95°
∠АСВ=180°-95°-70°=15°
∠ВСМ=∠АСВ=15° (по условию)
∠СВМ=180°-95°=85° как смежные угол с ∠АВС
∠СМВ=180°-85°-15°=80°
∠DMK и ∠СМВ - вертикальные ⇒ ∠DMK=80°
α=∠МКР и ∠DMK односторонние , в сумме дают 180° ⇒
α=180°-80°=100°
22. Продлим АС до пересечения с d₁ и d₂ .
В ΔАВЕ угол ∠ВАЕ=90° , так как он смежный с прямым углом ЕАС .
Так как ∠ВЕА=30° , то второй острый угол ΔАВЕ равен 60° ,
∠АВЕ=60° .
Так как d₁ ║ d₂ , то внутренние накрест лежащие углы равны ⇒
∠КМС=∠АВЕ=60°
∠КСМ - смежный с ∠КСА ⇒ ∠КСМ=180°-80°=100°
В ΔКСМ угол ∠СКМ=180°-100°-60°=20°
∠СКМ=∠МКР=20° по условию ,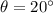 .
.
Угол α смежен с углом ∠СКМ ⇒ α=180°-20°=160°