В двух сосудах объёмом по `40` литров каждый, содержится (в сумме) `50` литров концентрированной кислоты. Первый сосуд доверху доливают водой, и содержимое тщательно перемешивают. После этого второй сосуд доверху наполняют смесью из первого сосуда. Оказалось, что во втором сосуде содержится на `21,2` литра чистой кислоты больше, чем в первом. Найдите первоначальное содержание кислоты в первом сосуде.
Пошаговое объяснение:
Задача №1.
Я, если честно, не понимаю формулировку "запиши ответ между корнями".
Но зато я попробую тебе решить данное уравнение.
Воспользуемся дискриминантом.
Вот формула:
x1,2 = ±b ± /2а
/2а
Где: b - второй коэффициент(который мы берем с противоположным знаком); а - это первый коэффициент(он же старший коэффициент); с - свободный член.
Подставим данные:
x1,2 = 7 ±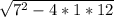 /2*1 = 7 ±1/2
/2*1 = 7 ±1/2
Тогда:
x1 = 4
x2 = 3
Задача №2
Ну для начала 7 умножим на 2 и получим 14.
Тогда имеем:
2^2 - 14 + 12.
От нас требуется извлечь корень из этого выражения.
Задача №3.
2 в квадрате = 4
Получили:
x^2 - 7x + 12 = 4
Переносим все вправо с изменением знака на противоположный.
x^2 - 7x + 8 = 0
Используя дискриминант, получаем следующие корни:
x1 =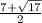
x2 = 7 - корень из 17 поделить на 2
Пусть в книге х страниц. В первый день Петя прочитал 0,4х страниц (40 % = 0,4; чтобы найти дробь от числа, надо это число умножить на дробь), во второй день - 0,6(х - 0,4х) страниц (60% остатка, 60 % = 0,6; осталось не прочитанными х - 0,4х), в третий - 144 страницы. Всего страниц в книге (0,4x + 0,6(x - 0,4x) + 144) страницы или x страниц. Составим уравнение и решим его.
0,4x + 0,6(x - 0,4x) + 144 = x;
0,4x + 0,6 * 0,6x + 144 = x;
0,4x + 0,36x - x = - 144;
- 0,24x = - 144;
x = - 144 : (- 0,24);
x = 600 (стр)
ответ. 600 страниц.