Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале - график расположен выше оси абсцисс. Функция отрицательна - график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна - график функции возрастает, отрицательна - убывает.
6. Выпуклость, вогнутость.
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна - график функции выпукл вверх. Отрицательна - график функции выпукл вниз.
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график.
Вы не поставили знаки возведения в степень (не забывайте их, иначе выражение совсем непонятно- приходится гадать, что за действие там было- умножение или возведение в степень).
Вот это выражение со знаками возведения в степень:
(x^2 - 6x + 9) + (5y - 3)^2 + (4z + 5)^4 = 0
А записав это же в поле уравнение (кнопка ), получим как на бумаге:
Решаем:
Отсюда получаем, что все три слагаемых должны быть равны нулю:
Считаем заданное выражение:
ответ: вариант 4
Задание 2
В тексте задачи опечатка- сравнивается время второго пешехода со вторым же. Если предположить, что правильный текст такой: "За сколько времени первый расстояние АВ", то имеем вот что:
Обозначим величины:
S - расстояние от A до B
t1 - время в пути первого пешехода
t2 - время в пути второго пешехода
v1 - скорость первого пешехода
v2 - скорость второго пешехода
Считаем что они двигались равномерно (не меняя скорости).
Первый и второй до точки встречи шли 3 часа. За это время они суммарно полное расстояние S. Запишем это, вычисляя путь каждого через его скорость и время (3 ч):
Запишем скорости пешеходов через путь и время каждого и подставим в уравнение выше.
Т.к. , то можем поделить обе части уравнения на :
Выразим время t2 через t1 (они связаны по условиям задачи), и подставим это выражение вместо t2 в уравнение:
Умножим обе части уравнения на :
(при этом нужно указать, что )
(ч)
(ч)
Значение 1 ч не подходит по условиям задачи (оно меньше 3 ч).
А значение 7,5 ч - подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или 2,5), но отсутствует среди вариантов ответа (если только вы первый вариант не записали с очередной ошибкой- 7 вместо 7,5).
То есть, в таком виде задачи, ответ будет- нет верных вариантов.
Решение будет подходить под эти варианты, только если предположить, что в тексте задачи вообще всё перепутано, и правильный текст на самом деле звучит как то так:
"Два пешехода вышли одновременно навстречу друг другу – первый из пункта А, второй из пункта В. Они встретились через три часа. За сколько времени первый расстояние АВ, если он пришёл в пункт В на 2,5 часа раньше, чем второй пришёл в пункт А."
В этом случае получим такое решение:
Т.к. , то можем поделить обе части уравнения на :
Умножим обе части уравнения на :
(при этом нужно указать, что )
(ч)
(ч)
Значение -1,5 ч не подходит по условиям задачи (здесь отрицательное время не имеет смысла).
Значение 5 ч -подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или -2,5) и присутствует среди вариантов ответа.
ответ: вариант 3
ВЫВОД: сверьте текст задания с исходным- если при наборе действительно были допущены указанные мной ошибки, то вариант решения я привёл выше (и, в следующий раз проверяйте текст перед отправкой задания).
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале - график расположен выше оси абсцисс. Функция отрицательна - график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна - график функции возрастает, отрицательна - убывает.
6. Выпуклость, вогнутость.
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна - график функции выпукл вверх. Отрицательна - график функции выпукл вниз.
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пошаговое объяснение:
Задание 1
Вы не поставили знаки возведения в степень (не забывайте их, иначе выражение совсем непонятно- приходится гадать, что за действие там было- умножение или возведение в степень).
Вот это выражение со знаками возведения в степень:
(x^2 - 6x + 9) + (5y - 3)^2 + (4z + 5)^4 = 0
А записав это же в поле уравнение (кнопка ), получим как на бумаге:
), получим как на бумаге:
Решаем:
Отсюда получаем, что все три слагаемых должны быть равны нулю:
Считаем заданное выражение:
ответ: вариант 4
Задание 2
В тексте задачи опечатка- сравнивается время второго пешехода со вторым же. Если предположить, что правильный текст такой: "За сколько времени первый расстояние АВ", то имеем вот что:
Обозначим величины:
S - расстояние от A до B
t1 - время в пути первого пешехода
t2 - время в пути второго пешехода
v1 - скорость первого пешехода
v2 - скорость второго пешехода
Считаем что они двигались равномерно (не меняя скорости).
Первый и второй до точки встречи шли 3 часа. За это время они суммарно полное расстояние S. Запишем это, вычисляя путь каждого через его скорость и время (3 ч):
Запишем скорости пешеходов через путь и время каждого и подставим в уравнение выше.
Т.к.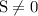 , то можем поделить обе части уравнения на
, то можем поделить обе части уравнения на 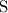 :
:
Выразим время t2 через t1 (они связаны по условиям задачи), и подставим это выражение вместо t2 в уравнение:
Умножим обе части уравнения на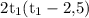 :
:
(при этом нужно указать, что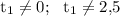 )
)
Значение 1 ч не подходит по условиям задачи (оно меньше 3 ч).
А значение 7,5 ч - подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или 2,5), но отсутствует среди вариантов ответа (если только вы первый вариант не записали с очередной ошибкой- 7 вместо 7,5).
То есть, в таком виде задачи, ответ будет- нет верных вариантов.
Решение будет подходить под эти варианты, только если предположить, что в тексте задачи вообще всё перепутано, и правильный текст на самом деле звучит как то так:
"Два пешехода вышли одновременно навстречу друг другу – первый из пункта А, второй из пункта В. Они встретились через три часа. За сколько времени первый расстояние АВ, если он пришёл в пункт В на 2,5 часа раньше, чем второй пришёл в пункт А."
В этом случае получим такое решение:
Т.к.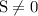 , то можем поделить обе части уравнения на
, то можем поделить обе части уравнения на 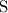 :
:
Умножим обе части уравнения на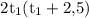 :
:
(при этом нужно указать, что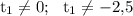 )
)
Значение -1,5 ч не подходит по условиям задачи (здесь отрицательное время не имеет смысла).
Значение 5 ч -подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или -2,5) и присутствует среди вариантов ответа.
ответ: вариант 3
ВЫВОД: сверьте текст задания с исходным- если при наборе действительно были допущены указанные мной ошибки, то вариант решения я привёл выше (и, в следующий раз проверяйте текст перед отправкой задания).