В одной бочке в 3 раза больше бензина, чем в другой. Если из первой бочки отлить 39 л бензина, а во вторую добавить 21 л, то бензина в бочках будет поровну. Сколько бензина в каждой бочке было первоначально?
Пошаговое объяснение:1. 10/20 * 6/19 * 4/18 - это целевая вероятность при одном сценарии (когда берётся наугад сначала изделие 1 сорта, потом 2, потом 3). Поскольку таких сценариев (3! = 6), а произведение везде будет одинаковое, то имеем ответ: 6 * (1/2 * 6/19 * 2/9)
2. Найти вероятность того, что обе детали бракованные.
Во-первых, надо допустить, что деталей бесконечное множество. То есть после взятия одной детали соотношение остаётся 40% к 60%. Если мы такое допустили, то можно приступить к расчёту.
Сумма вероятностей четырёх сценариев:
1. взяли две бракованных первого завода
2. взяли две бракованных второго завода
3. взяли бракованную первого завода и потом бракованную второго завода
4. взяли бракованную второго завода и потом бракованную первого завода
Пошаговое объяснение:
1)уравнение плоскости Q, проходящей через точки
А (–6; –4; 2);
В (5; –2; –1);
С (5; 6; –4);
для составления уравнения плоскости используем формулу
(x -(-6))(2*(-6) - (-3)*10) - (y -(-4))(11*(-6) -(-3)*11 ) + (z -2)(11*10 -2*11) = 0
18(x -(-6)) + 33(y - (-4)) + 88(z - 2) = 0
и вот мы получаем уравнение плоскости Q
Q : 18x + 33y + 88z +64 = 0
2) канонические уравнения прямой АВ. А(–6; –4; 2); В(5; –2; –1);
формула канонического уравнения прямой
наша формула прямой
3) уравнение плоскости G, проходящей через точку D(2; 8; 6) перпендикулярно прямой АВ
будем искать прямую в виде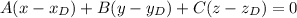
здесь А, В, С - координаты направляющего вектора.
поскольку G ⊥ АВ, то нормаль АВ будет направляющим вектором для G ⇒ s = n = (11, 2, -3)
и вот формула
G : 11y + 2y - 3z -20 =0
4) расстояние от точки D(2; 8; 6) до плоскости Q : 18x + 33y + 88z +64=0
для расчета нам потребуется
А = 18; В = 33; С = 88; D = 64;
Пошаговое объяснение:1. 10/20 * 6/19 * 4/18 - это целевая вероятность при одном сценарии (когда берётся наугад сначала изделие 1 сорта, потом 2, потом 3). Поскольку таких сценариев (3! = 6), а произведение везде будет одинаковое, то имеем ответ: 6 * (1/2 * 6/19 * 2/9)
2. Найти вероятность того, что обе детали бракованные.
Во-первых, надо допустить, что деталей бесконечное множество. То есть после взятия одной детали соотношение остаётся 40% к 60%. Если мы такое допустили, то можно приступить к расчёту.
Сумма вероятностей четырёх сценариев:
1. взяли две бракованных первого завода
2. взяли две бракованных второго завода
3. взяли бракованную первого завода и потом бракованную второго завода
4. взяли бракованную второго завода и потом бракованную первого завода
для 3 и 4 вероятность одинаковая.
ответ: 0.4 * 0.04 * 0.4 * 0.04 + 0.6 * 0.02 * 0.6 * 0.02 + 2 * (0.4 * 0.04 * 0.6 * 0.02)
Найти вероятность того, что обе детали бракованные изготовлены первым заводом.
Это у нас Сценарий 1.
ответ: 0.4 * 0.04 * 0.4 * 0.04