В одной строке записано восемь натуральных чисел. Докажите, что вы можете выбрать одно из этих чисел или несколько стоящих рядом чисел, сумма которых делится на 8.
если дробь не может быть представлена в виде конечной десятичной дроби, у нее указан в скобках период (это будет периодическая дробь) и далее напротив такой дроби стоит знак "-"
итак, из 10 данных дробей 6 могут быть представлены в виде конечной десятичной дроби
и это будет 6/10 от всех дробей или (6/10 = 3/5)
ответ
3/5 общего количества всех чисел, указанных в таблице, составляют дроби, которые можно представить в виде конечной десятичной дроби
Дан набор различных простых чисел. Может ли выполняться равенство
[Равенство (1) получается из приведенного в условии делением на ненулевое число n и переносом отрицательных слагаемых в правую часть]
Рассмотрим, например, левую часть:
И числитель, и знаменатель, очевидно, натуральные числа. Значит, левая часть представлена в виде обыкновенной дроби. Проверим, является ли она несократимой.
Пусть у числителя и знаменателя есть общий простой множитель, на который их можно сократить. Но тогда это одно из чисел [т.к. знаменатель представлен в виде произведения этих простых].
Итак, рассмотрим некоторое из этих чисел .
В сумме все слагаемые, кроме -ого, содержат в своем разложении на множители , а значит делятся на него. Остается слагаемое - но все сомножители в нем являются простыми числами, отличными от , а значит их произведение (т.е. само слагаемое) не делится на .
Тогда и сумма не делится на .
Перебрав все значения , получаем, что числитель и знаменатель не имеют общих простых множителей - а значит дробь несократима.
Аналогично получаем, что правая часть
- несократимая дробь.
То есть получили равенство двух положительных несократимых дробей с положительными знаменателями и и положительными числителями.
Но такое возможно лишь если числители и знаменатели равны между собой.
С другой стороны, например, знаменатель левой части делится на , а знаменатель правой нет, а значит совпадать они не могут. Противоречие.
3/5
Пошаговое объяснение:
переведем все дроби в десятичный вид.
если дробь не может быть представлена в виде конечной десятичной дроби, у нее указан в скобках период (это будет периодическая дробь) и далее напротив такой дроби стоит знак "-"
итак, из 10 данных дробей 6 могут быть представлены в виде конечной десятичной дроби
и это будет 6/10 от всех дробей или (6/10 = 3/5)
ответ
3/5 общего количества всех чисел, указанных в таблице, составляют дроби, которые можно представить в виде конечной десятичной дроби
Нет
Пошаговое объяснение:
Задачу можно переформулировать следующим образом:
Дан набор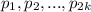 различных простых чисел. Может ли выполняться равенство
различных простых чисел. Может ли выполняться равенство 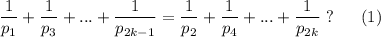
[Равенство (1) получается из приведенного в условии делением на ненулевое число n и переносом отрицательных слагаемых в правую часть]
Рассмотрим, например, левую часть:
И числитель, и знаменатель, очевидно, натуральные числа. Значит, левая часть представлена в виде обыкновенной дроби. Проверим, является ли она несократимой.
Пусть у числителя и знаменателя есть общий простой множитель, на который их можно сократить. Но тогда это одно из чисел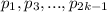 [т.к. знаменатель представлен в виде произведения этих простых].
[т.к. знаменатель представлен в виде произведения этих простых].
Итак, рассмотрим некоторое из этих чисел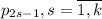 .
.
В сумме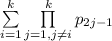 все слагаемые, кроме
все слагаемые, кроме  -ого, содержат в своем разложении на множители
-ого, содержат в своем разложении на множители 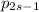 , а значит делятся на него. Остается слагаемое
, а значит делятся на него. Остается слагаемое 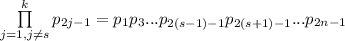 - но все сомножители в нем являются простыми числами, отличными от
- но все сомножители в нем являются простыми числами, отличными от 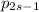 , а значит их произведение (т.е. само слагаемое) не делится на
, а значит их произведение (т.е. само слагаемое) не делится на 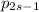 .
.
Тогда и сумма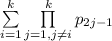 не делится на
не делится на 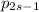 .
.
Перебрав все значения , получаем, что числитель и знаменатель не имеют общих простых множителей - а значит дробь несократима.
, получаем, что числитель и знаменатель не имеют общих простых множителей - а значит дробь несократима.
Аналогично получаем, что правая часть
То есть получили равенство двух положительных несократимых дробей с положительными знаменателями и
и 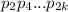 и положительными числителями.
и положительными числителями.
Но такое возможно лишь если числители и знаменатели равны между собой.
С другой стороны, например, знаменатель левой части делится на
делится на 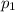 , а знаменатель правой
, а знаменатель правой 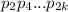 нет, а значит совпадать они не могут. Противоречие.
нет, а значит совпадать они не могут. Противоречие.
Значит, указанное равенство невозможно.