В окружности с центром в точке О проведена хорда АВ, длина которой равна длине радиуса. Перпендикулярно этой хорде проведен радиус ОК. Радиус ОК и хорда АВ пересекаются в точке М. Длина отрезка АМ равна 12,5 см. а) постройте чертеж по условию задачи- ; б) найдите длину хорды АВ - ;
в) вычислите длину радиуса- ;
г) найдите периметр треугольника АОВ -

Показать ответ

Ответ:

dianaism38

08.04.2020 06:12

Пропоную скласти таку казку про зиму для другого класу:

Прийшла на Землю Зима. Вона щодня з вірним товаришем Морозом розмальовувала віконця хат та трусила з неба снігом. Усі раділи. Сніговий шар слугував для рослин ковдрою. Так вони легше тірпли мороз.

Але одного разу сніг почав танути. Почалась сльота. Мороз поцікавився у подружки, що ж з нею сталось. Виявилось, що Зима прихворіла. Тому до нас у гості почала вриватися Весна прямо посеред січня. Але Мороз вилікував Зиму. І вулиці знову прикрасив пухкий сніжок.

0,0(0 оценок)

Ответ:

slappy337

26.10.2021 17:10

Будем разбивать на несколько случаев.

1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна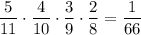 $\dfrac{5}{11}\cdot \dfrac{4}{10}\cdot \dfrac{3}{9}\cdot\dfrac{2}{8}=\dfrac{1}{66}$ . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна 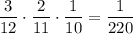$\dfrac{3}{12}\cdot\dfrac{2}{11}\cdot\dfrac{1}{10}=\dfrac{1}{220}$ . По теореме умножения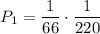 $P_1=\dfrac{1}{66}\cdot\dfrac{1}{220}$

2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна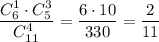 $\dfrac{C^1_6\cdot C^3_5}{C^4_{11}}=\dfrac{6\cdot10}{330}=\dfrac{2}{11}$ . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 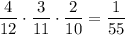$\dfrac{4}{12}\cdot\dfrac{3}{11}\cdot\dfrac{2}{10}=\dfrac{1}{55}$ . По теореме умножения: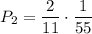 $P_2=\dfrac{2}{11}\cdot\dfrac{1}{55}$

3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: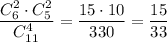 $\dfrac{C^2_6\cdot C^2_5}{C^4_{11}}=\dfrac{15\cdot10}{330}=\dfrac{15}{33}$ . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 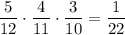$\dfrac{5}{12}\cdot\dfrac{4}{11}\cdot\dfrac{3}{10}=\dfrac{1}{22}$ . По теореме умножения :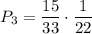 $P_3=\dfrac{15}{33}\cdot\dfrac{1}{22}$

4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна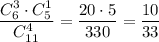 $\dfrac{C^3_6\cdot C^1_5}{C^4_{11}}=\dfrac{20\cdot5}{330}=\dfrac{10}{33}$ . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна 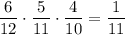$\dfrac{6}{12}\cdot\dfrac{5}{11}\cdot\dfrac{4}{10}=\dfrac{1}{11}$ . По теореме умножения: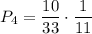 $P_4=\dfrac{10}{33}\cdot\dfrac{1}{11}$

5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: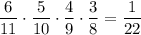 $\dfrac{6}{11}\cdot\dfrac{5}{10}\cdot\dfrac{4}{9}\cdot\dfrac{3}{8}=\dfrac{1}{22}$ . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 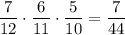$\dfrac{7}{12}\cdot\dfrac{6}{11}\cdot\dfrac{5}{10}=\dfrac{7}{44}$ . По теореме умножения: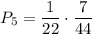 $P_5=\dfrac{1}{22}\cdot\dfrac{7}{44}$

Итого, по теореме сложения:

$P=P_1+P_2+P_3+P_4+P_5=\dfrac{1}{66}\cdot\dfrac{1}{220}+\dfrac{2}{11}\cdot\dfrac{1}{55}+\dfrac{15}{33}\cdot\dfrac{1}{22}+\\ \\ +\dfrac{10}{33}\cdot\dfrac{1}{11}+\dfrac{1}{22}\cdot\dfrac{7}{44}=\dfrac{427}{7260}\approx 0{,}0588$