В работе используется текст, выбранный студентом самостоятельно (авторский или скопированный из любого источника) и приложенный к работе.
Объем текста должен составлять одну страницу документа Microsoft Word при условии оформления по следующим правилам – шрифт Times New Roman 14, интервал 1,5, выравнивание по ширине, стандартные поля (левое 3 см, правое 1,5 см, верхнее и нижнее 2 см), автоматическая расстановка переносов, отсутствие дополнительного интервала между абзацами одного стиля, отступ первой строки 1,25 см.
В каждой строке текста необходимо подсчитать количество знаков без учета пробелов и количество гласных букв. Вычислить частоту гласных в строке с точностью до 0,05.
С полученным вариационным рядом частот выполнить следующие действия:
1) вычислить среднее арифметическое, размах, моду, медиану;
2) построить гистограмму распределения вариант данного ряда.

Пусть х- это кол-во книг на второй полке.

(х-4) _это кол-во книг на 1 полке.

(х+(х-4))*2 -это кол-во книг на 3 полке

                                       Составим уравнение

                               Х+(х-4)+(х+(х-4))*2=96

                                      6х-12=96

                                       6х= 108

                                       х= 108/6

                                       х=18 - это кол-во книг на 2 полке

1) 18-4= 14(кн.)-на 1 полке

2)(18+14)*2=64(кн.) - на 3 полке.

ответ 18,14,64

Можно проверить 14+18+64=96

Пошаговое объяснение:

Чертеж к решению задачи во вложении.Обозначим угол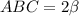 . Требуется найти синус угла АВС, т.е. .

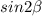Пусть t- величина одной части при делении стороны ромба точкой касания окружности. Тогда АР=3t, РВ=2t. 

По свойству ромба имеем:

1) BD - биссектриса угла АВС;

2) треугольник АОВ - прямоугольный с углом О=90 градусов.

По свойству касательной к окружности ОР-радиус и ОР перпендикуляен стороне АВ.

По свойству высоты прямоугольного треугольника

, т.е. 

Тогда ,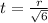 

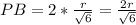
В прямоугольном треугольнике ОРВ по теореме Пифагора 

В теугольнике ОРВ: 

Наконец,

ответ: